数据结构与算法 - AC 自动机

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

前面已经介绍了暴力匹配算法、BM 算法、KMP 算法等几种单模式字符串匹配算法，在实际项目开发中，也经常会遇到多模式匹配需求，比如敏感词过滤功能，虽然使用单模式匹配算法也能够实现，但是下面介绍一种更加高效多模式匹配算法 - AC 自动机。

多模式匹配 - 暴力匹配

在介绍 AC 自动机算法实现之前，先看看使用暴力匹配算法如何实现多模式匹配，可以遍历所有模式串，逐一进行暴力匹配，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public Dictionary<string, List<int>> Match(string[] word, string text)
{
    Dictionary<string, List<int>> matched = new Dictionary<string, List<int>>();

    int M = text.Length;

    for (int i = 0; i < word.Length; i++)
    {
        string pattern = word[i];

        if (!matched.ContainsKey(pattern))
            matched.Add(pattern, new List<int>());

        int N = pattern.Length;

        for (int j = 0; j < M - N + 1; j++)
        {
            bool isMatch = true;
            for (int k = 0; k < N; k++)
            {
                if(pattern[k] != text[j+k])
                {
                    isMatch = false;
                    break;
                }
            }

            if(isMatch)
            {
                matched[pattern].Add(j);
            }
        }
    }

    return matched;
}

上面算法的时间复杂度为 O(KMN) 其中，K 为模式串的个数，M 为主串长度，N 为模式串平均长度。

用暴力匹配法解决多模式匹配很容易理解和实现，其时间复杂度为 O(MNK)，其中 M 为主串长度、N 为模式串平均长度、K 为模式串数量，下面看下如何进行改进呢，和 KMP 算法、BM 算法一样，目的都是希望减少字符比较次数，能够尽可能多的向后滑动，可能产生影响的，主要包括以下两点：

  • 已匹配字符串内容；
  • 各个模式串之间的内容有关系。

第一种情况之前算法中都已经介绍过了，第二种情况只针对多模式匹配，比如两个模式串 abc 和 bc，当 bc 不匹配时，abc 肯定也不匹配，因此就不需要再次进行比较了。

在清楚了问题所在之后，再来看如何解决这两个问题，第一问题可以采用 KMP 和 BM 算法来解决，重点关注如何解决第二个问题，上面算法实现中，我们采用字符串数组来存储所有的模式串，模式串之间都是独立存储，不能直接获取各个模式串之间的关系，所以首先需要解决模式串的存储问题，这里采用 Trie 单词树，不同的是，每个结点增加了一个失效指针。

构建单词树

在之前文章中已经详细的介绍了单词树的构造过程，所以这里就不再介绍，只关注失效指针的计算，下面直接给出 AC 自动机的代码框架和单词树的构建过程，后面再详细介绍各部分的实现原理：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
public class AC
{
    public class ACNode
    {
        public char key;
        public int value;
        public Dictionary<char, ACNode> children = new Dictionary<char, ACNode>();;

        // 失效指针
        public ACNode next;
        
        // 以该节点结尾的单词
        public string word;
    }

    private ACNode tree = new ACNode();

    public AC(string[] patterns)
    {
        if (patterns != null)
        {
            for (int i = 0; i < patterns.Length; i++)
            {
                Put(patterns[i]);
            }
            BuildFailurePointer();
        }
    }

    // 向字典树中插入模式串
    private void Put(string pattern)
    {
        ACNode node = tree;
        int idx = 0;
        while(idx != pattern.Length)
        {
            // 1. 查找是否存在对应的子结点
            if(!node.children.ContainsKey(pattern[idx]))
            {
                node.children.Add(pattern[idx], new ACNode()
                {
                    key = pattern[idx]
                });
            }

            // 2. 继续进行插入
            node = node.children[pattern[idx++]];
        }
        node.word = pattern;
        node.value++;
    }

    // 构建失效指针
    private void BuildFailurePointer(){}

    // AC 自动机匹配
    public Dictionary<string,List<int>> Match(string text){}
}

失效指针

在 KMP 算法中介绍过 KMP 失效指针的计算，其实 AC 自动机的失效指针和 KMP 是一样的，可以将 KMP 看做只有一个模式串的 AC 自动机。

在 AC 算法中，对于任一节点 A，从根节点到 A 的字符串为 str，A 的失效指针指向，与 str 所有后缀最长匹配的，所有模式串的前缀节点。

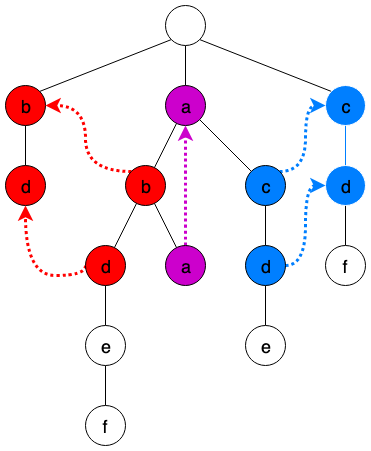
首先需要说明的是，所有结点的失效指针默认都指向根节点。

看上图中的 ‘acd’ 这条线，其后缀包括’d’、‘cd’，而在所有模式串中，与之匹配的最长的后缀为 ‘cd’，因此其失效指针指向 ‘cd’ 的 ‘d’ 结点。

计算失效指针

上面说了，可以将 KMP 看做是只有一个模式串的 AC 自动机，失效指针的计算也是基本相同的，唯一不同的在于，KMP 只需在单个模式串中计算，而 AC 则需要计算所有模式串，所以这里就不再介绍失效指针的原理，直接给出失效指针计算过程，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// 构建失效指针
private void BuildFailurePointer()
{
    // 利用队列，广度优先遍历单词树
    Queue<ACNode> queue = new Queue<ACNode>();

    tree.next = null;
    queue.Enqueue(tree);

    while (queue.Count > 0)
    {
        ACNode p = queue.Dequeue();

        // 遍历所有子结点
        foreach (var kvp in p.children)
        {
            ACNode child = kvp.Value;
            if (p == tree)
            {
                child.next = tree;
            }
            else
            {
                ACNode pFail = p.next;
                while(pFail != null)
                {
                    if (pFail.children.ContainsKey(child.key))
                    {
                        child.next = pFail.children[child.key];
                        break;
                    }
                    pFail = pFail.next;
                }

                if(pFail == null)
                {
                    child.next = tree;
                }
            }

            queue.Enqueue(child);
        }
    }
}

匹配实现

在了解了失效指针的构建过程之后，下面再看如何利用失效指针进行匹配，过程如下：

令 P 指向当前检查的指针，S 为主串，i 为主串字符指针。

  1. 从树的根节点开始检查，即 P = root，从主串第一个字符开始，即 i = 0；
  2. 从主串读取字符 s[i]；
  3. 遍历 P.children，是否存在于 s[i] 匹配的结点：
    • 若存在，将 P 指向该子结点，即 P = P.children[x]，继续：
      • 判断 P 是否表示单词结尾，若是，说明找到一个匹配的模式串，记录下来；
      • 判断 P 的失效指针是否指向一个单词结尾，若是，说明同样是匹配的模式串，记录下来；
      • 开始检查下一个字符，即 i++，执行步骤 2.
    • 若不存在，检查 P 是否为根结点：
      • 若是，i++，执行步骤 2；
      • 若不是，令 P 指向该结点的失效指针，继续步骤 3.

针对上面过程补充两点：

  • 找到匹配模式串，记录数据时，需要记录模式串在主串中的索引，该值等于 i - word.length + 1；
  • 当 P 子结点与字符s[i]不匹配，并且 P 为根节点时，说明模式串中，没有以字符s[i]开头的模式串，因此直接跳过。

将上述过程转换成代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
// AC 自动机匹配
public Dictionary<string, List<int>> Match(string text)
{
   Dictionary<string, List<int>> r = new Dictionary<string, List<int>>();

   ACNode p = tree;
   int M = text.Length;
   int i = 0;
   while (i < M)
   {
       char ch = text[i];

       if (p.children.ContainsKey(ch))
       {
           p = p.children[ch];

           if (p.word != null)
           {// 说明 P 结点为单词结尾
               if (!r.ContainsKey(p.word))
                   r.Add(p.word, new List<int>());

               r[p.word].Add(i - p.word.Length + 1);
           }

           if (p.next != null && p.next.word != null)
           {// 说明 p 的失效指针也是单词结尾
               if (!r.ContainsKey(p.next.word))
                   r.Add(p.next.word, new List<int>());

               r[p.next.word].Add(i - p.next.word.Length + 1);
           }

           // 继续处理下一个字符
           i++;
       }
       else
       {
           if (p != tree)
           {
               p = p.next;
           }
           else
           {
               i++;
           }
       }
   }

   return r;
}

总结

至此，多模式串匹配已经介绍完毕，还是看一下 AC 自动机的时间复杂度，其包括三部分：构造单词树、构造失效指针、字符串匹配，前两部分只在构造时执行一次，因此并不影响匹配时的效率，下面看下各部分的时间复杂度：

  • 构造单词树，这里和 trie 树一样为：O(KL) 其中 K 为单词的平均长度，L 为单词个数；
  • 构造失效指针，上限为：O(KN) 其中 K 为单词平均长度，N 为节点个数；
  • 匹配算法，影响外层循环次数的不确定因素为失效指针的跳转次数，这里按单词平均长度来计算，因此复杂度为 O(KM)，其中 K 为单词平均长度，M 为主串长度。

那么考虑一个问题，AC 是否一定比单模式匹配快？从时间复杂度来比较，这一点是肯定的，但是在特定的使用场景中，这个问题就不是那么容易回答了，从 AC 算法中可以发现，其优化核心是失效指针的跳转，而失效指针建立的前提是，模式串的后缀部分与前缀部分存在重合，因此，当给定的模式串中不存在这种重合的话，相当于这种优化是不起作用的，所以说，在实际使用中，还是要结合应用背景，选择合适的技术。