数据结构与算法 - KMP字符串匹配算法

在前面的文章中介绍了暴力匹配算法和 BM 算法，下面再介绍另一种匹配算法 - KMP 字符串匹配算法，之所以单独将它拿出来介绍，主要是它解释和理解起来都非常困难，为了更好的理解下面的内容，建议先看理解一下暴力匹配算法和 BM，这两者相对容易理解一些，可以当做一个预热。

KMP 匹配算法

KMP 算法和 BM 类似的是，两种算法那都是希望在出现不匹配字符时，能够尽可能多的向后进行滑动，这样就能有效的减少字符对比次数，从而降低时间复杂度，BM 的做法在前文已经介绍过了，下面来看下 KMP 是如何做的，先看下面一个例子：

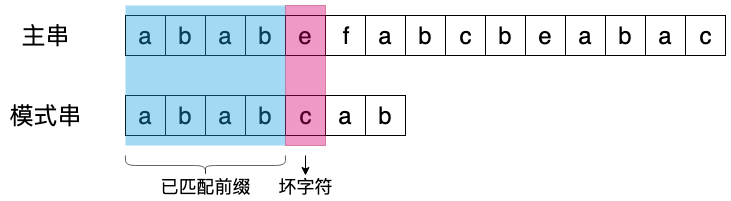
当遇到不匹配的字符时，就需要找到一种规律，能够向后滑动多个字符。或者有人可能想到直接将模式串，与不匹配字符的下一个位置对齐不就可以了，其实我在最初接触字符匹配算法时，也有这样的想法，但是这样可能会错过匹配项，比如下面的例子：

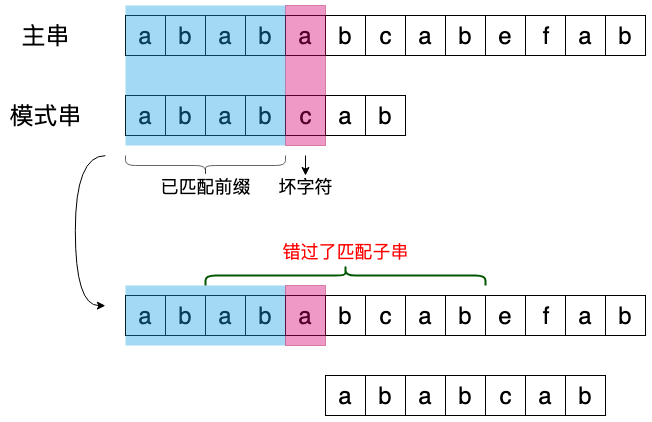
思考一下为什么上面例子中，会错过匹配的子串呢？这是因为，在已匹配前缀字符串 H 中，其后缀 “ab”，同样属于模式串 P 的前缀，这就可能错过匹配值。

好了，理解上面解释之后，最大滑动长度也就很清楚了，即将模式串 P滑动到，与已匹配前缀H的最长匹配后缀对齐，在上面例子中，就是将模式串与 H 后缀 “ab” 对齐：

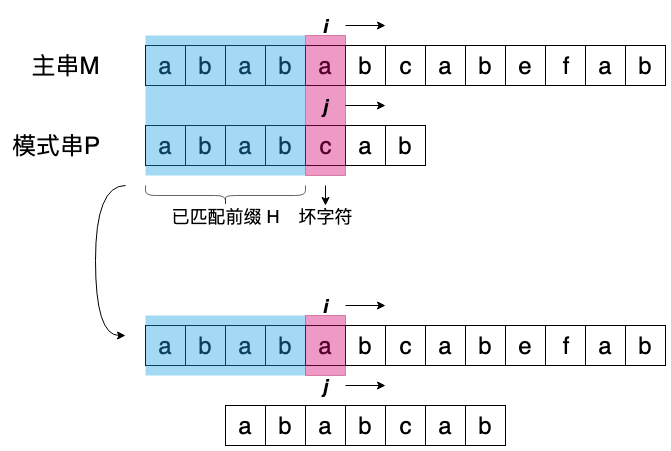
可以发现，整个滑动计算过程与主串没什么关系，这是因为我们处理的部分，是模式串与主串已经匹配的部分。既然如此，那么在进行匹配之前，我们能不能把匹配串 P 的所有前缀，以及前缀对应的最长匹配后缀处理好呢？

在 KMP 算法中采用一个数组来存储前缀信息，这个数组称为失效数组，数组的下标表示前缀尾字符下标（模式串中的下标），数组的值表示，在该前缀字符串中，最长匹配前缀的尾字符下标（前缀中的下标）。文字描述费劲看着也累，还是上面的例子，直接看图下表：

模式串前缀	前缀结尾字符下标	最长匹配前缀尾字符下标	数组
a	0	-1	next[0] = -1
ab	1	-1	next[1] = -1
aba	2	0	next[2] = 0
abab	3	1	next[3] = 1
ababc	4	-1	next[4] = -1
ababca	5	0	next[5] = 0
ababcab	6	1	next[6] = 1

那么这个 next 数组应该如何使用呢？还是看上面的例子，在模式串 P 的第 4 个字符出现不匹配，H 尾字符下标为 3，从表中可知 next[3] = 1，即 H 的前缀‘ab’与后缀‘ab’相同，因此，将模式串 P 前缀’ab’ 与 H 后缀’ab’对齐，相当于将 j 设置为 ‘ab’ 的下一个字符的下标，而改下标值等于 $next[3] + 1$。

上面这个过程可能有一些绕，和 BM 算法直接滑动主串不同，这里是滑动模式串，先假设用 i 表示主串字符索引，j 表示匹配串索引，不管滑动主串还是模式串，都是要比较 M[i]、P[j]，因此滑动匹配串就是更新 j 的值。

如果还是与有点不清楚，可以结合下面的 KMP 算法框架代码理解一下整个过程：

public int IndexOf(string s, string pat)
{
    int N = s.Length;
    int M = pat.Length;

    // 模式串索引指针
    int j = 0;

    for (int i = 0; i < N; i++)
    {
        // 如果出现不匹配字符，则滑动模式串，直到 s[i]、pat[j] 匹配
        while (pat[j] != s[i] && j > 0)
            j = next[j - 1] + 1;

        // 如果字符匹配，则继续检查主串和模式串下一个字符
        if (s[i] == pat[j])
        {
            j++;
        }

        if (j == M)
        {// 匹配成功
            return i - M + 1;
        }
    }

    return -1;
}

为什么模式串滑动要在 while 循环中，这是因为根据 next 数组进行滑动之后，s[i] 和 pat[j] 可能仍然不匹配，因此需要不断滑动，直到 s[i] 和 pat[j] 匹配，或者重新从匹配串起始进行匹配，具体过程见下图：

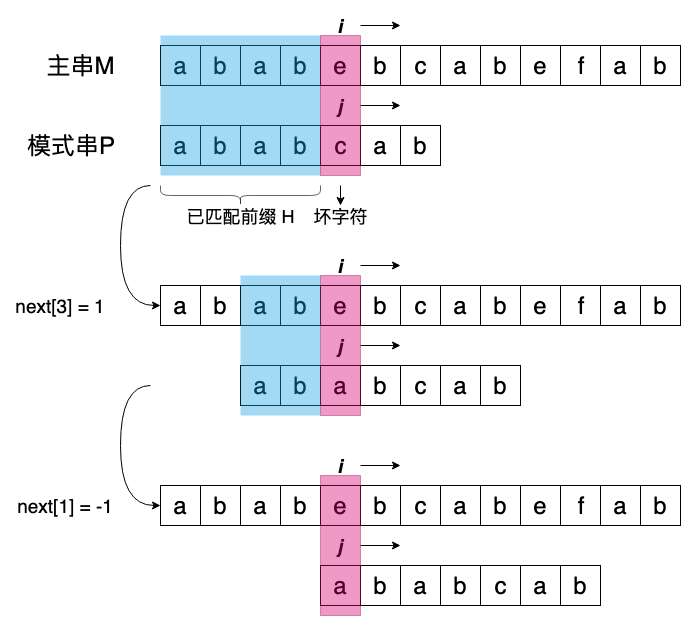
失效数组计算

上面已经理解了怎么用 next 数组，下面一个重要问题就是怎么计算 next 数组，还是以模式串‘ababcab’为例，比如要计算 next[3] 的值，最粗暴的方法时找到所有的前缀，然后逐一检查是否有对应后缀与之匹配，next[3] 对应的子串为 ‘abab’：

前缀	匹配后缀	前缀尾字符索引
aba	/	-1
ab	ab	1
a	/	-1

可以看到最长的匹配后缀为‘ab’，因此 next[3] = 1。这样的计算方式比较低效，原因在于当我们计算 next[4] 时，对于 next[3] 中计算的需要重新计算一遍，所以算法优化的重点在于如何根据 next[k-1] 计算 next[k] 的值。

根据 next[k-1] 计算 next[k] 分为以下几种情况:

首先说第一种情况，next[k-1]最长匹配前缀尾字符索引为 i，如果 next[k] 与 next[i+1] 匹配，此时 next[k] 的最长匹配的前缀尾字符索引为 $i+1$，还是看下面例子：

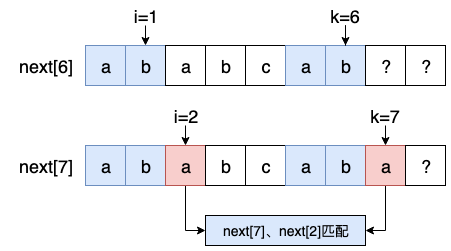
上面的情况还算比较简单，但是当 next[k] 和 next[i+1] 不相等时，情况就变得比较复杂了，还是以模式串‘abcababcab’为例，来看下应该如何处理这种情况：

next 失效数组为:

前缀	匹配后缀	前缀尾字符索引
abcababca	/	-1
abcababc	/	-1
abcabab	/	-1
abcaba	/	-1
abcab	abcab	4
abca	/	-1
abc	/	-1
ab	ab	1
a	/	-1

当下一个字符为 ‘c’ 时，如下图所示：

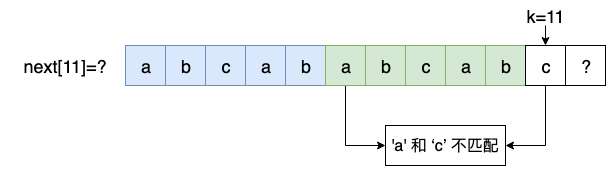
因为’a’、‘c’ 不匹配，所以不能像上面情况那样进行处理，即最长匹配后缀不是‘abcab’+‘c’，因此就需要考虑次长匹配后缀，从上面表中可知，次长匹配后缀为 ‘ab’，而‘ab’的下一个字符也是‘c’，所以 next[11] 的最长匹配后缀为 ‘abc’。

我们不能根据查表来获取次长匹配后缀，因此，下面问题就是如何找到次长匹配后缀，这里需要理解两点：

次长匹配后缀属于最长匹配后缀的一部分；
最长匹配前缀、最长匹配后缀两者是相同的。

基于以上两点，查找次长匹配后缀，就等价于从最长匹配后缀中，找出其最长匹配后缀，这样问题就变成了递归查找最长匹配后缀。这句话理解起来可能有点绕，还是继续上面的例子，最长匹配后缀为’abcab’，该字符串的最长匹配后缀为‘ab’。

可以配合下面代码理解一下上面两种情况的处理：

private int[] GetNexts(string s, int m)
{
   int[] nexts = new int[m];
   nexts[0] = -1;
   int k = -1;
   for (int i = 1; i < m; i++)
   {
       while (k != -1 && s[k + 1] != s[i])
       {
           k = nexts[k];
       }

       if (s[k + 1] == s[i])
           k++;

       nexts[i] = k;
   }
   return nexts;
}

总结

KMP 算法解释和理解起来确实非常困难，在理解过程中，可以动手画画来辅助理解。KMP 算法的空间复杂度为 O(M)，其中 M 为模式串长度；而时间复杂度分为O(M+N)，其中 M 为模式串长度，N 为主串长度。