数据结构与算法 - 单词查找树

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

平时在进行上网搜索时，都会有搜索提示功能，能够根据我们输入，自动的给出相应的提示内容，那么这个功能应该如何来实现呢，当搜索词库数据量很少时，采用什么办法效率上可能差别不大，但是随着词库的不断增长，查询效率就是我们需要考虑的问题了，单词查找树就是这么一种解决方案。

单词树的表示

比如现在我们希望实现一个查找单词的 App，下面看下如何使用单词查找树来实现，首先要解决的问题就是单词存储，单词查找树，顾名思义，就是用树来保存单词的信息，下图展示一个单词查找树：

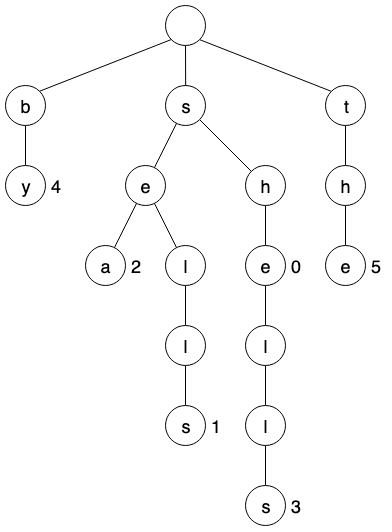
上图中，使用单词树存储了如下的单词（这里我们称之为’键’）：

键 值
by 4
sea 2
sells 1
she 0
shells 3
the 5

通过观察上面的单词树，可以发现一些特点：

  • 链接各个字符结点组成单词；
  • 单词的最后一个字符结点记录着单词的值；
  • 每个字符结点只有一个父节点，可以保护多个子节点。

这些特点和之前见过的一些树差不多，明显不同的是一些结点会记录对应单词的值，这个值是什么含义，怎么计算的？带着疑问继续下面的学习。

单词树的查找操作

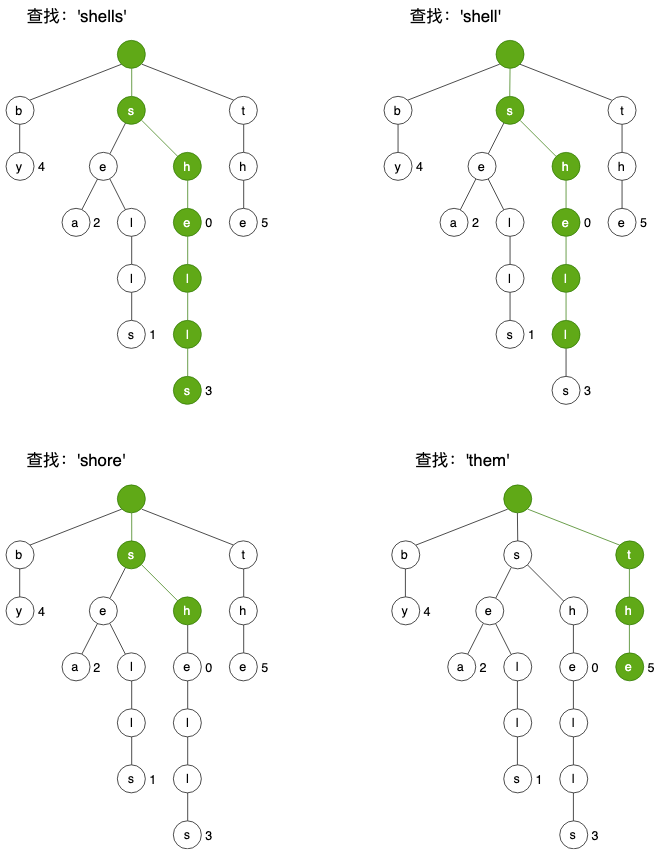
如何在单词树种进行查找，流程其实非常简单，比如在上面树种查找单词“shells”：

  1. 从根节点出发，在其子节点中查找第一个字符’s’；
  2. 找到’s’对应的结点之后，在其子节点中继续查找第2个字符’h’，如此递归，直到找到最后一个字符对应结点，或者子节点中不存在对应的字符链接，这里可能会遇到3中情况：
    1. 尾字符对应结点的值非空，比如查找’shells’、‘she’；
    2. 尾字符对应结点的值为空，比如查找’shell’；
    3. 在子节点中没有找到对应字符链接，比如查找’shore’、‘them’。

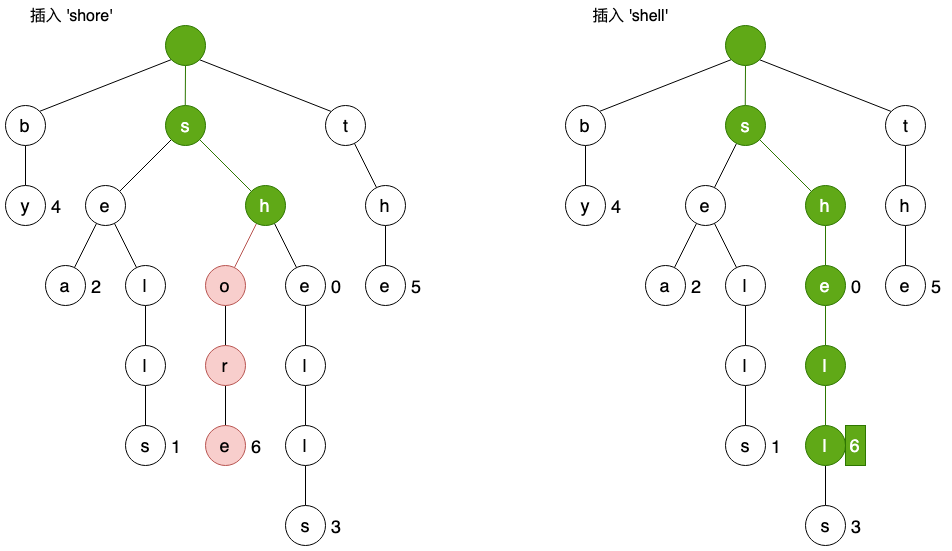
单词树的插入操作

在向单词树中插入新单词时，为了确定各个字符的插入位置，需要进行先查找，查找时可能遇到2种情况：

  • 在子节点中没找到字符的链接，比如插入‘shore’、‘them’；
  • 找到了尾字符对应的节点，比如插入‘shell’。

单词树的删除操作

从单词树中删除单词时，首先需要查找单词所对应的尾节点，这里有以下几种情况：

  1. 未找到单词所对应的尾结点，直接返回；
  2. 找到单词所对应的尾结点，然后置空该结点的值，下面处理方法分2中情况：
    1. 该尾结点没有子结点，删除该结点，继续尝试删除父节点；
    2. 该尾结点包含子结点，直接返回。

单词树的前缀匹配查找操作

在进行搜索提示时，需要查找指定前缀的词，这个过程和单词树的查找比较类似，这里直接上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
using System;
using System.Collections;
using System.Collections.Generic;
using System.Text;

public class TrieST<Value>
{
  public class Node
  {
      public char key;
      public Value value;
      public Dictionary<char, Node> children = new Dictionary<char, Node>();
  }

  // 根结点
  private Node tree = new Node();

  // 查找键对应的节点
  public Node Get(string key)
  {
      Node node = tree;
      int id = 0;
      while (id != key.Length)
      {
          if (node == null)
              return null;
          else
          {
              node = node.children[key[id]];
              id++;
          }
      }
      return node;
  }

  // 向树中添加键值
  public void Put(string key, Value val)
  {
      Node node = tree;
      int id = 0;
      while (id != key.Length)
      {
          if (!node.children.ContainsKey(key[id]))
          {
              node.children.Add(key[id], new Node()
              {
                  key = key[id]
              });
          }

          node = node.children[key[id]];

          id++;
      }
      node.value = val;
  }

  // 从树中删除对应的键值
  public void Delete(string key)
  {
      Node node = tree;
      int id = 0;
      System.Collections.Generic.Stack<Node> link = new System.Collections.Generic.Stack<Node>();
      bool findTail = true;
      while (id != key.Length)
      {
          if (node.children.ContainsKey(key[id]))
          {
              node = node.children[key[id]];
              link.Push(node);
              id++;
          }
          else
          {
              findTail = false;
              break;
          }
      }

      if (findTail)
      {
          node.value = default(Value);
          if (node.children.Count > 0)
              return;
          else
          {
              link.Pop();
              Node parent = link.Peek();
              parent.children.Remove(node.key);
              while (link.Count > 0 && parent.children.Count == 0 &&
                    parent.value.Equals(default(Value)))
              {
                  node = parent;
                  parent = link.Pop();
                  parent.children.Remove(node.key);
              }
          }
      }
  }

  // 找到指定前缀的键值
  public List<string> GetKeyWithPrefix(string prefix)
  {
      List<string> l = new List<string>();
      Node node = Get(prefix);
      if (node == null)
          return l;

      System.Collections.Generic.Stack<object> stack = new System.Collections.Generic.Stack<object>();
      stack.Push(node);
      stack.Push(prefix);

      while (stack.Count > 0)
      {
          string pref = stack.Pop() as string;
          Node x = stack.Pop() as Node;

          if (x == null) continue;
          if (!x.value.Equals(default(Value)))
              l.Add(pref);

          foreach (var kvp in x.children)
          {
              stack.Push(kvp.Value);
              stack.Push(string.Concat(pref,kvp.Key));
          }
      }
      return l;
  }
}

性能

  • 时间复杂度：在单词树中查找对应键的值，最坏情况下的时间复杂度为键长度加1；
  • 空间复杂度：对于字母表大小为 R、包含 N 个随机键的单词树，键的平均长度为 W，结点的链接总数在 RN ~ RNW 之间，所以有如下规律：
    • 当所有键均较短时，链接总数接近于 RN；
    • 当所有键均较长时，链接总数接近于 RNW；
    • 空间复杂度与 R 大小紧密相关。

总结

上面介绍了单词树 Trie，该数据结构常用来解决从大量词库中查找指定前缀的单词，比如网站的搜索功能，它能够最多搜索次数等于前缀的长度，是一种非常高效的结构，其比较适合键长较短的情景，当键长比较大时，占用的空间将会比较大。

除了上面的介绍的单词树之外，还有三向单词树，与Trie 不同，它是的每个结点只有三个子结点，在键比较长或者字符集比较大时，空间复杂度要比 Trie 树低很多，更加适合 Unicode 字符集。