数据结构与算法 - 字符串匹配

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

在日常开发中，经常会和字符串打交道，字符串匹配功能的使用频率也很高，比如 C# 中的 IndexOf()、Python 的 find()，它们背后实现就是字符串匹配算法，字符串匹配算法多种多样，如暴力匹配算法（BF），BM 算法、RK 算法、KMP 算法，本节主要介绍暴力匹配算法、BM 算法。

暴力匹配算法

字符串匹配是要解决如下问题：有字符串 A、B，要在 A 中找到子串 B，其中 A 称为主串，B 称为模式串。暴力匹配算法是最简单粗暴的解决方法，它的思想是这样的：

  1. 将 B 看做一个可以滑动的窗口，初始时将 B 与 A 的起始位置对齐；
  2. 然后检查重合部分是否匹配，不匹配则将 B 向后滑动一个位置；
  3. 直到完全匹配或 A、B 末尾重合。

用图来表示是这样的：

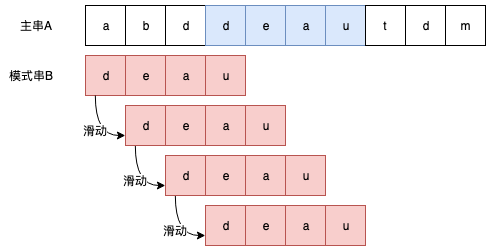
代码实现也比较简单：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
-- bf 暴力匹配算法
-- t 主串
-- n 模式串
function BFMatch(t,n)
  if #t < #n then
    return -1
  end
  
  for i=1,#t-#n+1 do
    local matched = true
    for j=1,#n do
      if t:byte(i+j-1) ~= n:byte(j) then
        matched = false
        break
      end
    end

    if matched then
      return i
    end
  end
  
  return -1
end

暴力匹配算法在最坏情况下需要进行 n-m 滑动，每次要比较 m 个字符，因此时间复杂度为 $O(MN)$，虽然时间复杂度比较高，但是在实际开发中也是比较常用，主要原因在于一般情况下主串不会太长，BF 算法在匹配成功之后就会结束计算，平均时间复杂度要更低；另外一个原因是 BF 算法实现比较简单。

BM 算法

Boyer-Moore 字符串匹配算法简称 BM 算法，它是一种启发式算法，在字符匹配的过程中，会根据不匹配字符在模式串中的位置，确定模式串如何进行滑动，先看下面一个例子，先看下匹配过程示意图，结合图在稍作解释。

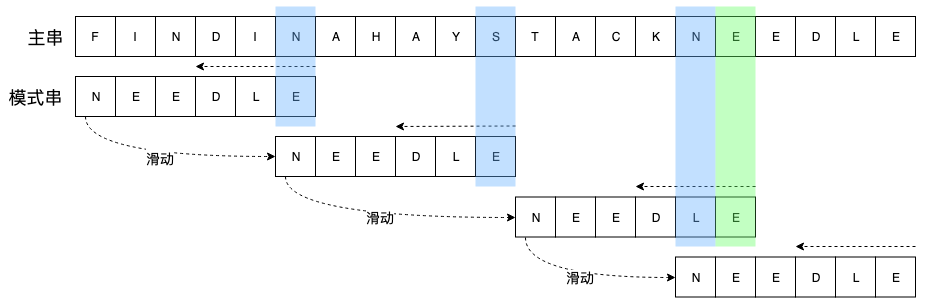
  1. 与暴力匹配算法不同，bm 是从右向左检查模式串，首先对比模式串最后一个 E 和主串第6个字符 N，发现不匹配，向后滑动模式串，让模式串中最右侧的 N 与主串 N 对齐；
  2. 再次自右向左对比模式串和主串，发现 S 和 E 不匹配，再次滑动，因为 S 在模式串中不存在，所以将模式串滑动到 S 的下一个位置；
  3. 再次自右向左对比，主串中的 E 和模式串相匹配，比较下一个字符 N 和 L，发现不匹配，向后滑动模式串，使模式串 N 与主串对齐；
  4. 再次自右向左对比，发现主串与模式串匹配。

通过上面的过程可以发现，模式串的滑动与不匹配字符在模式串中的位置有关，具体是什么样的关系？如果整清楚这个问题了，那么 bm 算法也就清楚了，下面详细介绍 bm 算法的实现。

BM 算法实现分为两个阶段：

  1. 记录字符表中各个字符在模式串中最后出现的位置；
  2. 子串匹配。

还是结合上面的例子来看下这两个步骤是如何实现的，首先，记录字符表中的字符在模式串中最后出现位置，因为每次不匹配都要用到这个位置，所以查询起来必须非常高效，可以采用记录方案有两种，第一种对于只存在 ASCII 字符的模式串，可以使用 256 大小的数组来存储；第二种对于存在 Unicode 字符的模式串，可以使用散列表。这里采用第一种方式，实现也很简单：先将数组所有值置为 -1，然后从左向右遍历模式串设置数组，直接上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public int[] RecordRights(string pattern)
{
  int[] rightIndex = new int[256];
  for (int i = 0; i < rightIndex.Length; i++)
  {
      rightIndex[i] = -1;
  }

  for (int i = 0; i < pattern.Length; i++)
  {
      rightIndex[pattern[i]] = i;
  }
  return rightIndex;
}

子串匹配，整个过程其实是向右滑动模式串的过程，我们用 $i$ 记录模式串与主串对齐的位置，用 j 表示从右向左遍历模式串的索引，比较主串的 $M[i+j]$ 和 模式串的 $N[j]$，匹配则继续向右比较，不匹配时会遇到三种情况：

  1. 不匹配字符不在模式串中，此时将模式串与不匹配字符的下一个字符对齐，即 i 增加 $j+1$；
  2. 不匹配字符在模式串中，我们找到它在模式串中出现的最后位置 $k$，使模式串与之对齐，即 i 增加 $j-k$;
  3. 对于第2中情况，如果$j-k < 0$，即最后的位置在 j 的右侧，如果还按照第2种情况处理，就会使模式串向左滑动，这并不是我们期望的，所以此时将模式串向右滑动1个位置，即 i 增加 1。

前面两种情况在上面的例子中都有遇到，特别说明一下第三种情况，如下图所示：

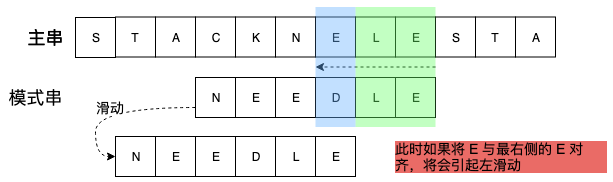
在整清楚上面三种情况之后，代码实现相对容易一些，完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
public class BoyerMoore
{
    private int[] rights;
    private string pattern;

    public BoyerMoore(string pattern)
    {
        this.pattern = pattern;
        this.rights = RecordRights(pattern);
    }

    private int[] RecordRights(string pattern)
    {
        int[] rightIndex = new int[256];
        for (int i = 0; i < rightIndex.Length; i++)
        {
            rightIndex[i] = -1;
        }

        for (int i = 0; i < pattern.Length; i++)
        {
            rightIndex[pattern[i]] = i;
        }
        return rightIndex;
    }

    public int Search(string text)
    {
        int N = text.Length;
        int M = pattern.Length;
        int skip = 0;
        for (int i = 0; i <= N-M; i+= skip)
        {
            skip = 0;
            for (int j = M-1; j >= 0; j--)
            {
                if(text[i+j] != pattern[j])
                {
                    skip = j - rights[text[i + j]];
                    if (skip < 1) skip = 1;
                    break;
                }
            }

            if (skip == 0)
                return i;
        }
        return -1;
    }
}

总结

上面介绍了两种字符串匹配算法，BF 暴力匹配算法、BoyerMoore 匹配算法，两个算法的执行过程，可以看做模式串窗口在主串上进行滑动的过程，其中 BF 每次滑动的步长为 1，而 BM 滑动的步长需要由不匹配字符和模式串来确定。

BF 的优点在于非常简单粗暴，易于理解和实现，BM 算法在主串非常大时能够极大的提高查找效率，在最坏情况下，两者的时间复杂度都为 $O(MN)$，一般情况下 BF 的复杂度为$O(N)$，BM 为$O(N/M)$。

除了BF 和 BM 算法之外，其他匹配算法还有 Rabin-Karp算法、KMP 算法，两者都是非常高效的匹配算法，尤其是 KMP 算法，感兴趣的可以看这篇文章。

匹配算法不止用在字符串匹配，类似的匹配也都可以使用这种思想，比如在一个设备操作考核中，从用户的操作序列中，匹配一个特定序列，来判断用户是否操作正确。