数据结构与算法 - 最小生成树

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

数据结构与算法 - 最小生成树

在之前学习了无向图和有向图，本节再介绍一种常用的图结构-加权无向图，从名字上就可以看出来，它是无向图的一种，与无向图不同的是，加权无向图的边带有权重，这个权重可以表示任意内容，比如地图中的距离、电网中成本等等。在这些问题中，通常比较关心如何成本最小化，下面就看看如何通过最小生成树来解决此类问题。

什么是生成树？图的生成树是一颗包含其所有顶点的无环连通子图；
什么是最小生成树？它是生成树的一种，其特点是所有边权值的和最小。

加权无向图数据结构

在介绍最小生成树实现算法之前，首先需要了解加权无向图如何表示，上一篇中介绍了无向图的表示方法，加权无向图与之类似，只不过多了一个权重值，因此需要定义边结构体，详细代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
public class EdgeWeightedGraph
{
    public class Edge : IComparable<Edge>
    {
        private int w;

        public int Either { get; private set; }
        public float Weight { get; private set; }

        public Edge(int v, int w, float weight)
        {
            this.Either = v;
            this.w = w;
            this.Weight = weight;
        }

        public int CompareTo(Edge other)
        {
            return Weight.CompareTo(other.Weight);
        }

        public int Other(int vertex)
        {
            if (vertex == this.Either) return this.w;
            else if (vertex == this.w) return this.Either;
            else throw new System.ArgumentException("Inconsistent edge");
        }
    }

    public int VertexCount { get; private set;}
    public int EdgeCount { get; private set; }

    private HashSet<Edge>[] adj;

    public EdgeWeightedGraph(int vCount)
    {
        this.VertexCount = vCount;
        this.EdgeCount = 0;
        this.adj = new HashSet<Edge>[vCount];
        for (int i = 0; i < adj.Length; i++)
        {
            this.adj[i] = new HashSet<Edge>();
        }
    }

    public void AddEdge(Edge e)
    {
        int v = e.Either;
        int w = e.Other(v);
        this.adj[v].Add(e);
        this.adj[w].Add(e);
        this.EdgeCount++;
    }

    // 获取顶点的所有相邻顶点
    public IList<Edge> GetAdjs(int v)
    {
        return new List<Edge>(this.adj[v]);
    }

    // 获取顶点的度
    public int GetDegree(int v)
    {
        return this.adj[v].Count;
    }

    // 获取所有顶点最大的度
    public int GetMaxDegree()
    {
        int maxDegree = 0;
        for (int i = 0; i < this.adj.Length; i++)
        {
            if (this.adj[i].Count > maxDegree)
                maxDegree = this.adj[i].Count;
        }
        return maxDegree;
    }

    // 获取所有顶点的平均度
    public float GetAvgDegree()
    {
        return 2.0f * this.EdgeCount / this.VertexCount;
    }
}

与无向图的表示主要有两点不同：

  1. 边表示方式不同：加权无向图单独定义了边结构体；
  2. 邻接表存储方式不同：使用 HashSet 顶点邻接边。

Prim 算法

介绍的第一种最小生成树计算方法叫做 Prim 算法，它的思想是这样：

  1. 将树的顶点分为未访问、已访问两部分，初始时已访问部分只有一个顶点 A；
  2. 然后访问顶点 A 的相邻顶点，从相邻顶点中找出未访问且边权重最小的顶点 B，将 B 加入到已访问部分；
  3. 递归的对 B 执行 第 2 步操作，直到所有顶点访问完成。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
public class LazyPrimMST
{
  // 标记顶点是否已经访问过
  private bool[] marked;

  // 最小生成树的边
  private System.Collections.Generic.Queue<EdgeWeightedGraph.Edge> mst;

  // 小顶堆，维护顶点相邻的边，方便高效的从中找出
  // 权重最小的边
  private Heap<EdgeWeightedGraph.Edge> pq;

  public LazyPrimMST(EdgeWeightedGraph graph)
  {
      this.marked = new bool[graph.VertexCount];
      this.mst = new System.Collections.Generic.Queue<EdgeWeightedGraph.Edge>();
      this.pq = new Heap<EdgeWeightedGraph.Edge>();

      // 初始时，将第一个顶点标记为已访
      // 然后遍历其邻边
      Visit(graph, 0);

      while (!pq.IsEmpty())
      {
          // 获取权重值最小的边
          EdgeWeightedGraph.Edge e = pq.RemoveMin();

          int v = e.Either;
          int w = e.Other(v);

          // 如果两个顶点都已经访问过，则不做任何处理
          if (this.marked[v] && this.marked[w])
              continue;

          // 将最小边添加到生成树种
          mst.Enqueue(e);

          // 继续递归遍历
          // v、w 两者必有一个已经访问过
          if (!this.marked[v]) this.Visit(graph, v);
          if (!this.marked[w]) this.Visit(graph, w);
      }
  }

  private void Visit(EdgeWeightedGraph graph, int v)
  {
      this.marked[v] = true;
      var adjs = graph.GetAdjs(v);
      for (int i = 0; i < adjs.Count; i++)
      {
          // 如果相邻的顶点还未访问，将之添加到小顶堆中
          if (!this.marked[adjs[i].Other(v)])
              pq.Insert(adjs[i]);
      }
  }

  public IEnumerable<EdgeWeightedGraph.Edge> Edges()
  {
      return mst;
  }
}

对于一副包含 V 个顶点、E 条边的连通加权无向图来说，LazmPrim 实现能够在 $E\log{E}$ 的时间复杂度内完成最小生成树算法，但是 LazyPrim 算法还存在一定的改进空间，先看下下图 LazyPrim 的执行过程：

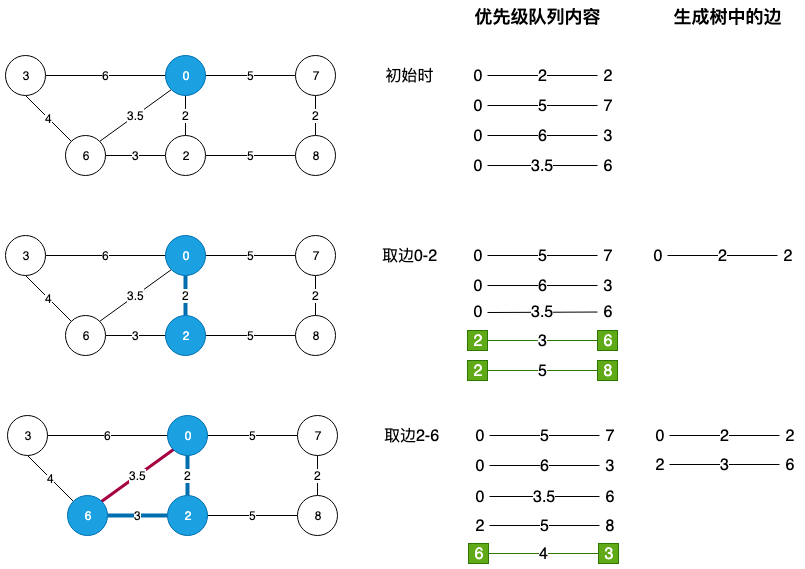
那么问题出在哪里呢？先简单说一下上面的执行过程：

  1. 初始时将第一个元素 0 添加的生成树中，并且将相邻边添加到优先级队列中；
  2. 然后从优先级队列中取出最小边 0-2，将 2 添加到生成树中，并且将 2 相邻的边添加到优先级队列（标绿部分）；
  3. 重复第 2 步骤，这次取出的是边 2-6，将 6 添加到生成中，此时问题出现了，因为之前将边 0-6 添加到了优先级队列，而此时0、6都是生成树的顶点，所以0-6就失效了（因为0-2-6已经保证了0-6之间的连通性，所以就不需要额外的边添加到最小生成树中了），下次从优先级队列中取出 0-6 时就做了无用功。

通过上面过程 LazyPrim 算法的问题就很明显了，解决该问题的关键在于向优先级队列中插入边时，需要检测哪些边需要插入、哪些不需要，详细的过程这里就不赘述了，直接看代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
public class PrimMST
{
  private EdgeWeightedGraph.Edge[] EdgeTo;
  private float[] DistTo;
  private bool[] marked;
  private IndexMinPQ<float> pq;

  public PrimMST(EdgeWeightedGraph graph)
  {
      this.EdgeTo = new EdgeWeightedGraph.Edge[graph.VertexCount];
      this.DistTo = new float[graph.VertexCount];
      this.marked = new bool[graph.VertexCount];
      pq = new IndexMinPQ<float>();

      for (int i = 0; i < graph.VertexCount; i++)
      {
          DistTo[i] = float.MaxValue;
      }

      DistTo[0] = 0.0f;
      pq.Insert(0, 0.0f);
      while (!pq.IsEmpty())
          Visit(graph, pq.RemoveMin());
  }

  private void Visit(EdgeWeightedGraph graph,int v)
  {
      this.marked[v] = true;

      var adjs = graph.GetAdjs(v);
      for (int i = 0; i < adjs.Count; i++)
      {
          int w = adjs[i].Other(v);
          if (this.marked[w])
              continue;

          if(this.DistTo[w] > adjs[i].Weight)
          {
              // 更新最佳边
              this.EdgeTo[w] = adjs[i];

              this.DistTo[w] = adjs[i].Weight;
              if (pq.Contains(w)) pq.Change(w, DistTo[w]);
              else pq.Insert(w, DistTo[w]);
          }
      }
  }

  public IEnumerable<EdgeWeightedGraph.Edge> Edges()
  {
      List<EdgeWeightedGraph.Edge> mst = new List<EdgeWeightedGraph.Edge>();
      for (int i = 0; i < this.EdgeTo.Length; i++)
      {
          mst.Add(EdgeTo[i]);
      }
      return mst;
  }
}

总结

加权无向图是对无向图的一种扩展，它的边带有权重属性，最小生成树是包含所有节点，并且边权重之和最小的子树，它常被用来解决成本最小化的问题，介绍了 Prim 最小生成树算法，包括 Lazy 实现和优化实现，它的时间复杂度为$E\log{E}$，另外常用的最小生成树算法 Kruskal 算法。