数据结构与算法 - 图

本节介绍一种新的数据结构-图，图的应用非常广泛，例如社交网络中的好友关系、计算机网络连接关系、地图道路等等，图的种类多种多样，根据不同的业务需求，选择不同的图，这里介绍4中最重要的图模型：无向图（简单连接）、有向图（连接有方向）、加权图（连接带有权重）、加权有向图（连接既有方向又包含权重）。

无向图

无向图的定义是这样的：

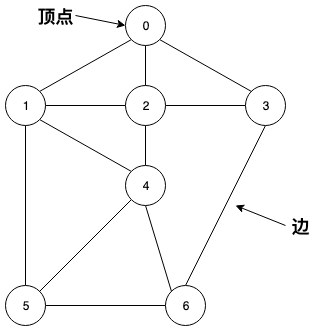
图是由一组顶点和一组连接两个顶点的边组成的。

一般来说，顶点叫什么我们并不关心（地图中的路口、社交网络中的人、电路中的元器件都是顶点），我们只需要有一种方法来指代这些顶点，一般用 0 到 V-1 来表示一张包含 V 个顶点的图。

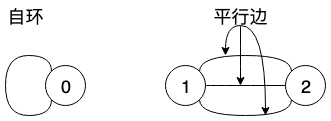
有两种特殊的情况：

• 自环：一个顶点，一条边头尾都连接到顶点；
• 平行边：头尾是同一对顶点的两条边称为平行边。

与图相关的几个术语：

• 相邻顶点：如果两个顶点通过一条边相连时，那么这两个顶点是相邻的，并称这条边依附于这两个顶点；
• 顶点的度：与顶点相连的边的数量，叫做顶点的度；
• 路径：路径是由边顺序连接的一组顶点；
• 连通图：图中任意两个顶点都至少有一条路径连接，这种图叫做连通图；
• 环：至少包含一条边，并且起点和终点相同的路径。

如果将图看做是物理存在的物体，比如绳结为顶点、绳子为边，那么拎起任意一个绳结，连通图将会是一个整体，而非连通图将会散落成好几部分。

表示方法

图是用来解决实际问题，所以表示图的数据结构应该能够解决绝大部分问题，其应该具备以下两点：

• 能够容纳各种规模的数据，小到几十个顶点，大到百万个顶点；
• 操作起来效率要高。

一般可供选择的表示方法由：邻接矩阵、边数组、邻接表数组，下面就具体看一下这三种方法各有什么优缺点。

邻接矩阵

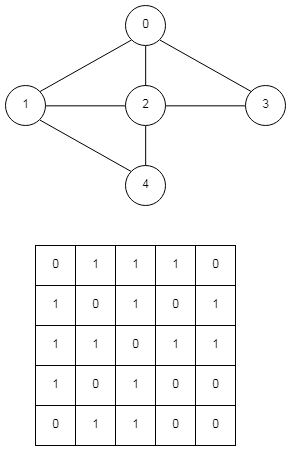
邻接矩阵是基于二维数组的，如果图$V$中的顶点$i$、$j$有边连接，对应矩阵的第i行、j列标记为1，所以对于包含 $n$ 个顶点的图，就需要 $n x n$ 的二维数组，这就会造成极大的空间浪费，不满足上面的第一点要求；另外，邻接矩阵无法表示平行边。

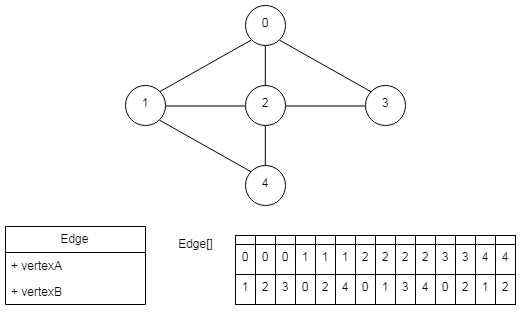
边数组

这种方法是定义边结构体，其中包含所依附的顶点，将图所有的边存储到数组中，这种方式对于某些操作（比如查找顶点相连的边）效率比较低，需要遍历所有的边才能够完成，不满足上面的第二点要求。

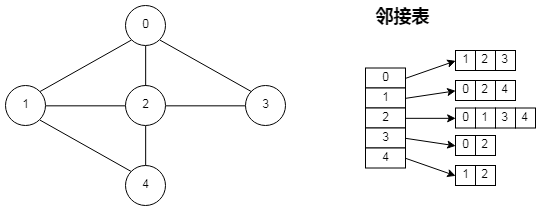
邻接表

邻接表是顶点索引的数组，数组元素为指向链表的指针，链表中存储着该顶点相邻的顶点索引。采用这种方式能够满足上面的两点要求，对于一个包含 V 个顶点 E 条边的图，所需的空间大小为 V + E；查找相连顶点的时间复杂度为 $O(1)$；为顶点增加新连接的时间复杂度与该顶点的度成正比；并且能够表示平衡边。

如果顶点不是整数，没有办法作为索引，这种情况可以采用散列表替换数组和链表，比如 C# 中的 Dictionary、HashSet。

无向图基础操作

这里只实现图相关的基本操作，采用邻接表表示方式，包括：

• 添加边；
• 获取顶点个数；
• 获取边数；
• 获取相邻顶点；
• 计算顶点的度；
• 计算所有顶点的最大度数；
• 计算所有顶点的平均度数。

为了实现起来简便，这里没有实现添加顶点、删除顶点、删除边，顶点也表示为整数。

直接上代码：

public class Graph
{
    // 顶点个数
    private readonly int VertexCount;

    // 边个数
    private int EdgeCount;

    // 邻接表
    private List<int>[] adj;

    public Graph(int v)
    {
        this.VertexCount = v;
        this.EdgeCount = 0;
        this.adj = new List<int>[v];
        for (int i = 0; i < v; i++)
        {
            this.adj[i] = new List<int>();
        }
    }

    // 添加边
    public void AddEdge(int v, int w)
    {
        this.adj[v].Add(w);
        this.adj[w].Add(v);
        this.EdgeCount++;
    }

    // 获取顶点数
    public int GetVertexCount()
    {
        return this.VertexCount;
    }

    // 获取边数
    public int GetEdgeCount()
    {
        return this.EdgeCount;
    }

    // 获取顶点的所有相邻顶点
    public IList<int> GetAdjs(int v)
    {
        return new List<int>(this.adj[v]);
    }

    // 获取顶点的度
    public int GetDegree(int v)
    {
        return this.adj[v].Count;
    }

    // 获取所有顶点最大的度
    public int GetMaxDegree()
    {
        int maxDegree = 0;
        for (int i = 0; i < this.adj.Length; i++)
        {
            if (this.adj[i].Count > maxDegree)
                maxDegree = this.adj[i].Count;
        }
        return maxDegree;
    }

    // 获取所有顶点的平均度
    public float GetAvgDegree()
    {
        return 2.0f * this.EdgeCount / this.VertexCount;
    }
}

搜索算法

在介绍完了图的一些基础算法之后，继续介绍图的搜索算法，图的搜索算法用途非常广泛，最典型的是寻路，将地图抽象为图结构，给定起点、终点，搜索出一条可行的路径；再比如社交网络中有个著名的六度分隔理论，该理论认为世界上两个互不认识的人，最多只需要6个中间人就能够联系在一起。

图的搜索算法很多，比如下面要介绍的深度优先搜索、广度优先搜索，以及 A、IDA 等启发式算法，为了将算法和图的实现解耦，这里采用策略模式，将各个算法封装为单独的类。

广度优先搜索

广度优先搜索(Breadth-First-Search、BFS)是暴力搜索的一种，很多复杂的搜索算法都是基于广度优先搜索演变而来的，它的流程是这样的，从起始顶点开始：

1. 遍历顶点 $A$ 的相邻顶点$A_i \in [A_0,A_n]$；
2. 如果$A_i$已经访问过，则跳过，否则记录下在搜索路径上离 $A_i$ 最近的顶点 $A$，并标记 $A_i$ 已经访问过；
3. 当 $A$ 相邻的顶点遍历完成之后，开始遍历 $A_i \in [A_0,A_n]$ 的相邻的节点，重复 1 过程。
4. 直到图中所有的顶点遍历完成之后，搜索结束。

广度优先搜索是一种地毯式搜索，借助下面动画理解一下搜索过程。

虽然看起来流程很简单，但是实现起来还是略微有些麻烦，还是直接上代码，通过代码理解一下：

public class BFSSearch
{
  private int Start;

  // 从起点到达该顶点的路径上的最后一个顶点
  // 通过递归的方式，就能找到到起点的路径
  private int[] EdgeTo;

  // 是否存在从起点到该顶点的路径
  private bool[] Marked;

  public BFSSearch(Graph g,int s){
      this.Start = s;
      this.Marked = new bool[g.GetVertexCount()];
      this.EdgeTo = new int[g.GetVertexCount()];

      this.BFS(g, s);
  }

  private void BFS(Graph g,int s)
  {
      // 保存待遍历的节点
      Queue<int> queue = new Queue<int>();

      // 标记起点 - 已访问
      Marked[s] = true;

      queue.Enqueue(s);
      while(queue.Size > 0)
      {
          int ver = queue.Dequeue();

          // 获取相邻节点
          IList<int> adjs = g.GetAdjs(ver);
          for (int i = 0; i < adjs.Count; i++)
          {
              // 相邻节点
              int adjVer = adjs[i];

              // 如果已经访问过，则直接跳过
              if (Marked[adjVer]) continue;

              // 一路遍历到这里，说明存在到这里的路
              // 另一个意义就是标记该节点已经访问过，避免后续重复访问
              this.Marked[adjVer] = true;

              // 记录一下这条路上离我最近的点
              this.EdgeTo[adjVer] = ver;

              // 将相邻节点的相邻节点添加到队列
              // 本层级的相邻节点遍历完之后，进行下一级遍历
              queue.Enqueue(adjVer);
          }
      }
  }

  // 是否存在从 s 到 v 的路径
  public bool HasPathTo(int v)
  {
      return this.Marked[v];
  }

  // 找到从 s 到 v 的路径
  public IEnumerable<int> PathTo(int v)
  {
      // 不存在路径
      if (!HasPathTo(v))
          return null;

      System.Collections.Generic.Stack<int> stack = new System.Collections.Generic.Stack<int>();
      int prev = v;
      while(prev != this.Start)
      {
          stack.Push(prev);
          prev = this.EdgeTo[prev];
      }
      stack.Push(this.Start);

      return stack;
  }
}

深度优先搜索

广度优先搜索是层层递进的地毯式搜索，深度优先搜索则截然相反，它的搜索方式就好像一个人在走迷宫，沿着一条路一直走，直到无路可走，才回头选择其他的路。

深度优先搜索的描述比 BFS 还要简单，只需要递归地遍历图所有顶点，在访问任一顶点时：

1. 如果已被标记为已搜索，则跳过，否则继续搜索；
2. 将该顶点标记为已搜索；
3. 递归的遍历该顶点的相邻顶点。

可以通过下面动画来理解一下这一过程：

实现代码如下：

public class DFSSearch
{
  private int Start;
  private int[] EdgeTo;
  private bool[] Marked;

  public DFSSearch(Graph g, int s)
  {
      this.Start = s;
      this.EdgeTo = new int[g.GetVertexCount()];
      this.Marked = new bool[g.GetVertexCount()];
      this.DFS(g, s);
  }

  private void DFS(Graph g, int s)
  {
      this.Marked[s] = true;

      IList<int> adjs = g.GetAdjs(s);
      for (int i = 0; i < adjs.Count; i++)
      {
          // 已经访问过，则直接跳过
          if (this.Marked[adjs[i]])
              continue;

          this.EdgeTo[adjs[i]] = s;
          this.DFS(g, adjs[i]);
      }
  }

  public bool HasPathTo(int v)
  {
      return this.Marked[v];
  }

  public IEnumerable<int> PathTo(int v)
  {
      if (!this.HasPathTo(v))
          return null;

      System.Collections.Generic.Stack<int> stack = new System.Collections.Generic.Stack<int>();
      while (v != this.Start)
      {
          stack.Push(v);
          v = this.EdgeTo[v];
      }
      stack.Push(this.Start);

      return stack;
  }
}

有向图

有向图和无向图非常类似，唯一的区别在于有向图的边是有方向的，有向图的应用也非常广泛，比如表示食物链（动物之间的捕食关系基本都是单向的）、论文中的引用关系等。

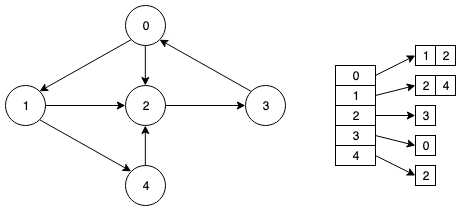
有向图是由一组顶点和一组有方向的边组成。

有向图的表示方法和无向图相同，都是采用邻接表。

有向图基础操作

与无向图的基本操作大致相同，不同的是添加边、删除边操作，另外有向图还会经常用到取反操作，就是将所有边的方向反向，下面直接上代码，与无向图相同的部分，这里就不列出来了。

// 添加边v->w
public void AddEdge(int v, int w)
{
   this.adj[v].Add(w);
   this.EdgeCount++;
}

// 获取反向图
public Digraph Reverse()
{
   Digraph reverse = new Digraph(this.VertexCount);
   for (int i = 0; i < this.VertexCount; i++)
   {
       for (int j = 0; j < this.adj[i].Count; j++)
       {
           reverse.AddEdge(j, i);
       }
   }
   return reverse;
}

有向图搜索算法

深度优先搜索和广度优先搜索也都适用于有向图，主要用于解决对象可达性判断，应用非常广泛，比如垃圾回收标记算法、有向图寻路等，可达性包含单点可达性、多点可达性：

单点可达性：在给定的一个起点、一个目标点之间，是否存在有向的路径；
多点可达性：在给定多个起点、一个目标点之间，是否存在有向的路径。

public class DirectedDFS
{
  private bool[] Marked;

  // 单点可达性
  public DirectedDFS(Digraph graph,int s)
  {
      this.Marked = new bool[graph.GetVertexCount()];
      this.DFS(graph, s);
  }


  // 多点可达性判断
  public DirectedDFS(Digraph graph,IEnumerable<int> ss)
  {
      this.Marked = new bool[graph.GetVertexCount()];
      foreach (var item in ss)
      {
          if (!this.Marked[item])
              this.DFS(graph, item);
      }
  }

  // 深度优先搜索
  private void DFS(Digraph graph,int s)
  {
      this.Marked[s] = true;
      var adjs = graph.GetAdjs(s);
      for (int i = 0; i < adjs.Count;i++)
      {
          if (!this.Marked[adjs[i]])
              this.DFS(graph, s);
      }
  }

  // 判断
  public bool IsReachable(int v)
  {
      return this.Marked[v];
  }
}

拓扑排序算法

有向图的另一个重要应用是解决调度问题，比如有一系列任务需要完成，每个任务可能都有前置执行条件，如何确定任务执行顺序，这里就可以采用拓扑排序来解决。

拓扑排序就是将有向图中的顶点进行排序，使得所有的边都从前面顶点指向后面的顶点。

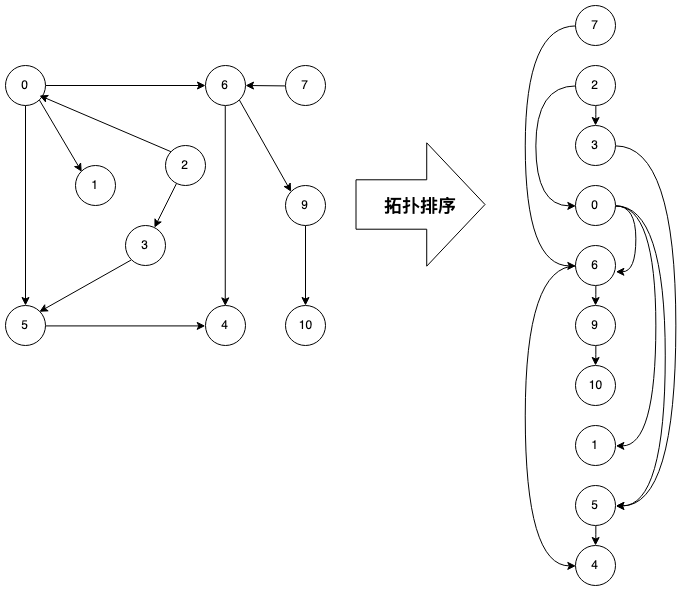
从定义结合图可以看出来，如果有向图中存在环，即图必须是有向无环图（DAG），是无法进行拓扑排序的，所以在进行拓扑排序之前，需要判断有向图中是否存在有向环。

有向环判断

有向环的判断需要使用深度优先搜索，过程就像一个人拿着绳子在走迷宫，走的过程中会不断放下绳子，如果遇到了死路则回退到最近的一个路口，退的过程中会将绳子收起来，然后继续选择其他路径前进，如果前进过程中发现地上有绳子，说明该迷宫中存在环，用代码实现如下：

public class DirectedCircle
{

  private bool[] Marked;
  private int[] EdgeTo;
  private bool[] IsInStack;
  private bool HasCirCle;
  private int CircleVertex;

  public DirectedCircle(Digraph graph)
  {
      this.Marked = new bool[graph.GetVertexCount()];
      this.EdgeTo = new int[graph.GetVertexCount()];
      this.IsInStack = new bool[graph.GetVertexCount()];
      for (int v = 0; v < graph.GetVertexCount();v++)
          if(!this.Marked[v])
              DFS(graph, v);
  }

  private void DFS(Digraph graph,int v)
  {
      this.Marked[v] = true;

      // 向前走，将绳子放下
      this.IsInStack[v] = true;

      var adjs = graph.GetAdjs(v);
      for (int i = 0; i < adjs.Count;i++)
      {
          // 遇到环了
          if (this.IsInStack[adjs[i]])
          {
              // 记录下环上的一个顶点
              this.CircleVertex = adjs[i];
              this.HasCirCle = true;
              return;
          }

          // 还未访问过
          if(!this.Marked[adjs[i]])
          {
              this.Marked[adjs[i]] = true;
              this.DFS(graph, adjs[i]);
          }
      }

      // 往回走，将绳子捡起来
      this.IsInStack[v] = false;
  }

  public bool HasCircle()
  {
      return this.HasCirCle;
  }
}

基于 DFS 的顶点排序

因为图的顶点是无序的，所以排序的目的就是希望按照某种特定的顺序来访问图的顶点，这里常用的排序主要有三种：前序、后续、逆后续。排序实现的思想是在 DFS 过程中，将每个顶点保存到一个数据结构中，然后遍历该结构就能遍历图所有顶点，遍历的顺序取决于数据结构性质和顶点插入时机。

• 前序：在递归调用之前，将顶点插入队列；
• 后续：在递归调用之后，将顶点插入队列；
• 逆后续：在递归调用之后，将顶点插入栈。

public class DepthFirstOrder
{
    private bool[] Marked;
    private System.Collections.Generic.Queue<int> PreOrder;
    private System.Collections.Generic.Queue<int> PostOrder;
    private System.Collections.Generic.Stack<int> ReversePostOrder;

    public DepthFirstOrder(Digraph graph)
    {
        this.Marked = new bool[graph.GetVertexCount()];
        this.PreOrder = new System.Collections.Generic.Queue<int>();
        this.PostOrder = new System.Collections.Generic.Queue<int>();
        this.ReversePostOrder = new System.Collections.Generic.Stack<int>();

        for (int i = 0; i < graph.GetVertexCount(); i++)
        {
            if (!this.Marked[i])
                this.DFS(graph, i);
        }
    }

    private void DFS(Digraph graph, int v)
    {
        // 前序：在递归调用之前，将顶点插入队列
        PreOrder.Enqueue(v);

        this.Marked[v] = true;
        var adjs = graph.GetAdjs(v);
        for (int i = 0; i < adjs.Count; i++)
        {
            if (!this.Marked[adjs[i]])
            {
                this.DFS(graph, adjs[i]);
            }
        }

        // 后续：在递归调用之后，将顶点插入队列
        PostOrder.Enqueue(v);

        // 逆后续：在递归调用之后，将顶点插入栈
        ReversePostOrder.Push(v);
    }

    public IEnumerable<int> Pre()
    {
        return this.PreOrder;
    }

    public IEnumerable<int> Post()
    {
        return this.PostOrder;
    }

    public IEnumerable<int> ReversePost()
    {
        return this.ReversePostOrder;
    }
}

拓扑排序

DAG 的拓扑排序为所有顶点的逆后序排列，，结合上面有向环判断和顶点排序算法，能够很容易的编写拓扑排序算法：

public class Topological
{
    private IEnumerable<int> order;
    private bool hasCircle;

    public Topological(Digraph graph)
    {
        DirectedCircle circle = new DirectedCircle(graph);
        this.hasCircle = circle.HasCircle();

        if (!hasCircle)
        {
            DepthFirstOrder dfo = new DepthFirstOrder(graph);
            this.order = dfo.ReversePost();
        }
    }

    // 拓扑序列
    public IEnumerable<int> Order()
    {
        return this.order;
    }

    // 是否为有向无环图
    public bool IsDAG()
    {
        return !hasCircle;
    }
}