数据结构与算法 - 二叉堆

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

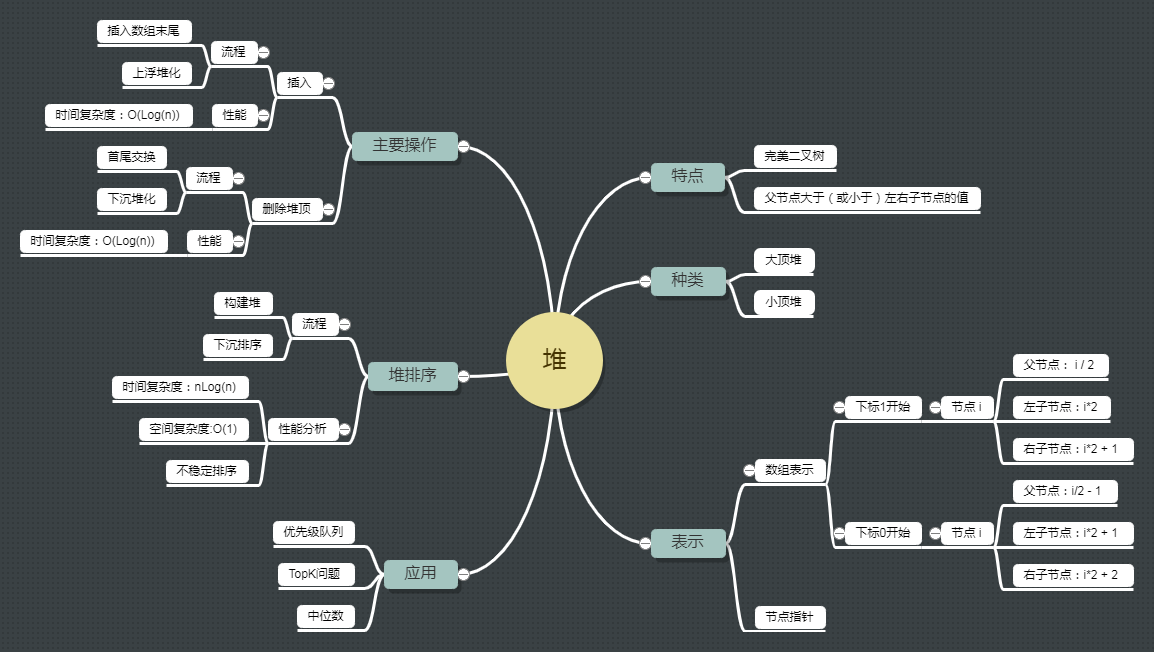
在之前的文章中学习了二叉搜索树以及红黑树，它们有个共同的特点是，对于任意节点都大于它的左子节点，小于它的右子节点。

本文介绍另一种形式的二叉树 - 二叉堆，它满足以下性质：

  • 二叉堆是完全二叉树
  • 对于任意节点，都大于等于（或小于等于）它的左右子节点

二叉堆得根为最大值的称作大顶堆，为最小值的称作小顶堆。

在前文介绍过树的表示方式，对于完全二叉树来说，比较适合采用数组来实现，本文中堆就是基于数组的实现，

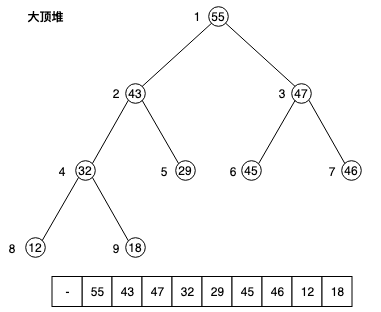
二叉堆的根节点存储在数组第2个位置，下标为0的位置空置，那么为什么没有采用之前介绍的从下标0开始呢，主要是方便父子节点下标换算，这样对于任意的节点 i：

  • 左子节点为 $2i$
  • 右子节点为 $2i + 1$
  • 父节点为 $i/2$

如果从数组的0开始，那么对于任意的节点 i：

  • 左子节点为:$2*i+1$
  • 右子节点为:$2*i+2$
  • 父节点为:$\frac{i}{2}-1$

堆化操作

堆在进行插入、删除的过程中，为了保证堆的特性，需要进行堆化(Heapify)，堆化分为两种：

  • 自下而上的堆化(上浮)，从指定节点开始，不断向上与父节点进行比较，如果大于父节点则交换，直到小于等于父节点或到达堆顶。
  • 自上而下的堆化(下沉)，从指定节点开始，不断向下与左右子节点中较大的值进行比较，如果比较大值小则交换，直到比较大值大或左右子节点不存在。

上浮堆化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/// <summary>
/// 自下而上进行上浮堆化
/// </summary>
/// <param name="i">其实索引</param>
private void Swim(int i)
{
    while (i > 1 && this.comparer.Compare(this.items[i], this.items[i / 2]) > 0)
    {
        T temp = this.items[i / 2];
        this.items[i / 2] = this.items[i];
        this.items[i] = temp;

        i = i / 2;
    }
}

下沉堆化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/// <summary>
/// 自上而下进行下沉堆化
/// </summary>
/// <param name="i">起始索引</param>
private void Sink(int i)
{
    while (i * 2 <= this.count)
    {
        // 找到左右子节点中较大的一个
        int maxChild = i * 2;
        if (this.comparer.Compare(this.items[i * 2], this.items[(i * 2) + 1]) < 0)
        {
            maxChild++;
        }

        if (this.comparer.Compare(this.items[maxChild], this.items[i]) < 0)
        {
            break;
        }

        T temp = this.items[maxChild];
        this.items[maxChild] = this.items[i];
        this.items[i] = temp;

        i = maxChild;
    }
}

堆的插入

插入操作流程：

  1. 向数组末尾插入新元素；
  2. 从插入位置进行上浮堆化。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public void Insert(T item)
{
    if(count == items.Length-1){
        // 堆满了，需要动态扩容
        return;
    }

    // 插入到数组
    items[++count] = item;

    int check = count;
    int parent = check / 2;

    // 存在父节点，并且比父节点大，则交换位置
    while(parent > 0 && comparer.Compare(items[check],items[parent]) > 0)
    {
        T temp = items[parent];
        items[parent] = items[check];
        items[check] = temp;

        check = parent;
        parent = parent / 2;
    }
}

堆的删除

这里只介绍删除堆顶元素，删除的流程是这样的：

  1. 将堆顶元素与最后一个元素进行交换；
  2. 删除最后一个元素；
  3. 自对顶开始进行下沉堆化。
1
2
3
4
5
6
7
8
9
10
public void RemoveMax()
{
   if (count <= 0) return;

   // 将堆顶元素交换到最后一个位置
   items[1] = items[count];
   items[count--] = default(T);

   Sink(1);
}

堆排序

之前文章介绍了冒泡、选择、插入、快排等排序算法，这里再介绍一种新的排序算法 - 堆排序，它的时间复杂度和快排、归并排序相同，都为$O(n{\log}n)$。

堆排序分为两个阶段：构造堆、下沉排序。

构造堆

构造堆有两种方式：上浮构造、下沉构造

上浮构造的实现思路是这样的，将数组划分两个分区：堆有序区、待插入区，遍历待插入区将所有元素插入到堆有序区中。

下沉构造的实现思路也是将数组划分为两个区：堆有序区、待插入区，与上浮不同的是，下沉是从下往上进行插入，这样做的好处是，下沉过程中，最下面一层的叶子节点没有子结点，所以不需要进行比较，因此比上浮的效率要高一点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public int[] BuildHeap(int[] n)
{
   int length = n.Length;
   for (int i = length / 2; i >= 1;--i)
   {
       // 下沉
       int node = i;
       while(i * 2 < length)
       {
           int maxChild = i * 2;
           if (n[maxChild] < n[maxChild + 1])
               maxChild++;

           if (n[node] > n[maxChild])
               break;

           int temp = n[node];
           n[node] = n[maxChild];
           n[maxChild] = temp;

           i = maxChild;
       }
   }
}

排序

在堆构造完成之后，形成一个大顶堆，即数组的第一个元素为最大的值，排序流程是这样：

  1. 从数组末尾开始遍历；
  2. 将元素与堆顶元素交换；
  3. 从堆顶开始向下进行下沉堆化。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public void Sort(int[] heap)
{
   int N = heap.Length - 1;
   for (int i = N; i >= 1; i--)
   {
       int node = i;

       int maxValue = heap[1];
       heap[1] = heap[node];
       heap[node] = maxValue;

       while(node * 2 < i)
       {
           int maxChild = node * 2;
           if (maxChild + 1 < i && heap[maxChild] < heap[maxChild + 1])
               maxChild++;

           if (heap[node] > heap[maxChild])
               break;

           int temp = heap[node];
           heap[node] = heap[maxChild];
           heap[maxChild] = temp;

           node = maxChild;
       }
   }
}

堆排序性能

堆排序的两个过程中，只需要常量的内存空间，空间复杂度为：$O(0)$。
时间复杂度为：$O(n\log{n})$
堆排序中存在头尾元素的交换，因此为不稳定排序。

堆排序和快速排序对比

堆排序和快速排序的时间复杂度都为$O(n\log{n})$，空间复杂度为:$O(0)$，都为不稳定排序。那为什么多数语言排序都采用快速排序呢，主要有两方面原因：

  1. 堆排序中的下沉操作要根据父节点访问子结点，这是一个非连续的内存访问，不利于内存缓存；
  2. 对于相同规模的数据，堆排序数据交换的次数要比快速排序多。

堆得应用

优先级队列

优先级队列也是队列的一种，与普通队列不同的是，出队的顺序按照优先级进行，优先级最高的最先出队，有多种方法来实现优先级队列，但是用的最多的还是堆，因为最小/最大的元素总是在堆顶，并且堆得插入、删除都非常的高效。优先级队列的应用非常多，比如霍夫曼编码、图的最短路径、最小生成树等等。

计算 TopK 问题

TopK 问题就是从一组数据里面选出最靠前的 K 个值，利用小顶堆可以非常容易的解决这个问题，解决流程是这样的：

  1. 创建一个大小为 K 小顶堆；
  2. 遍历数据集合，将元素与堆顶元素进行比较；
  3. 如果比堆顶值大，则将堆顶元素删除，然后将新元素插入到堆中；如果比堆顶值小，则继续遍历；
  4. 遍历完成之后，堆中的元素就是 TopK 元素。

伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function GetTopK(items)
{
    Heap h = new Heap();
    for a in items
    {
        if a > h.Top
        {
            h.RemoveMin();
            h.Insert(a);
        }
    }

    return h;
}

上面说的流程只针对静态集合，如果是支持插入删除的动态集合，那么就需要在插入时，将目标元素按照上述流程进行检测；如果时删除元素时，同样需要将之从小顶堆中删除。

计算中位数

中位数就是集合中间的那个数，对于规模为 n 的有序集合，如果 n 为奇数，则中位数为 $\frac{n}{2}+1$；如果 n 为偶数，中间位置有两个数，$\frac{n}{2}$、$\frac{n}{2}+1$，此时中位数可以是这两个中的任意一个。

首先分析一下中位数的特点：

  • 中位数将集合分为两个部分，在前半部分中最小，在后半部分中最大；
  • 前后两部分元素数量上是确定的。

如何用堆来解决中位数问题呢，使用两个堆来实现两个分区，小顶堆表示前半部分，大顶堆表示后半部分。集合个数为偶数时，小顶堆、大顶堆元素数量都为 $\frac{n}{2}$；集合个数为奇数时，小顶堆元素数量为 $\frac{n}{2}$，大顶堆元素数量为 $\frac{n}{2}+1$。

具体的处理流程如下：

  1. 创建小顶堆(前半部分) $H{min}$、大顶堆(后半部分) $H{max}$；
  2. 遍历集合元素，如果大于等于$H{min}$堆顶元素，则插入到$H{min}$中，否则插入到$H_{max}$中；
  3. 比较两个堆，是否满足元素数量上的要求，如果不满足，通过移动堆顶元素，来达到要求；
  4. 最终两个堆顶即为所求中位数。

其实不只是中位数，只要是满足中位数两个特点的问题（分两个区、每个区元素数量确定，求分界点），都可以采用上述思路来解决，比如计算 1/3、1/4 位置处的元素。

总结