数据结构与算法 - 红黑树

前面已经学习了跳表、散列表，它们的插入、删除、查找等操作是非常高效的，本章再介绍最后一种数据结构 - 红黑树，红黑树是二叉搜索树的改进，所以在介绍红黑树之前，先简单简单介绍一下二叉搜索树。

二叉搜索树

在之前的文章介绍了有根树的表示，其中介绍了有根树的两种表示方法，父子节点表示法和左孩子右兄弟表示法，对于二叉树的表示来说，这两种方式都可以，本节采用第一种表示方式，对其他方式感兴趣的可以参考前文。

二叉搜索树的特点

在之前介绍过二分查找算法，它是一种基于数组的非常高效的查找算法，最坏情况时间复杂度为$O(\log{n})$，本质上二叉搜索树也是二分思想的一种应用，它通过树的形式，使得二分更加的具象化：以当前节点为中点，分出左右两个子分支。

在二叉搜索树中，对于任一节点，具备如下特点：

它的值大于左子树所有节点
它的值小于右子树所有节点

二叉搜索树的插入

根据二叉搜索树的特点，当需要插入一个新节点时，从根节点开始遍历，和节点值进行比较，如果大于节点的值，则递归检查右子节点；如果小于节点的值，则递归检查左子节点；如果与节点的值相等，一般有几种处理方式：

插入失败，停止插入数据。
当做大于节点处理，插入右子树中。
当做小于节点处理，插入左子树中。

在使用时要根据自己的实际需求，选择适当的插入策略，并且其他操作（查找、删除）也都要遵守这种策略。在下面代码实现中，采取第二种策略，即插入到右子树中。

插入代码如下：

public void Insert(T t)
{
    if (tree == null)
    {
        tree = new BinaryTreeNode()
        {
            data = t
        };
        return;
    }

    BinaryTreeNode node = tree;
    while (node != null)
    {
        if (comparer.Compare(node.data, t) > 0)
        {
            if (node.leftChild == null)
            {
                node.leftChild = new BinaryTreeNode()
                {
                    data = t
                };
                break;
            }
            node = node.leftChild;
        }
        else
        {
            if (node.rightChild == null)
            {
                node.rightChild = new BinaryTreeNode()
                {
                    data = t
                };
                break;
            }
            node = node.rightChild;
        }
    }
}

从上面实现可以看出，新插入的节点，总是二叉树的叶节点。

二叉搜索树的删除

和新插入的节点总是叶节点不同，删除的节点可能在二叉树的任何位置，在删除节点之后，还必须保持二叉搜索树的特性，因此删除操作稍微有点麻烦，根据要删除节点的孩子节点数量，分为下面三种情况：

没有任何子节点，此时不需要额外操作
有一个子节点（左或者右），将要删除的节点的父节点指向子节点
有两个子节点，找到右子树的最小节点，将父节点指向该节点。

前两种情况比较容易理解，稍微解释一下第三种情况，二叉搜索树特性换一种理解方式：任一节点都是左右子树的分界点，因此当删除该节点时，就需要从剩余的子节点中，重新选取新的分界点，而所有的右子树结点都大于左子树结点，所以只需要从右子树中选取最小节点作为新分界点即可。（或从左子树选择最大的节点）

代码如下：

public void Delete(T t)
{
    if (tree == null)
        return;

    BinaryTreeNode node = tree;         // 要删除的节点
    BinaryTreeNode nodeParent = null;   // 要删除结点的父节点
    while (node != null)
    {
        int comp = comparer.Compare(t, node.data);
        if (comp < 0)
        {// t < node.data
            nodeParent = node;
            node = node.leftChild;
        }
        else if (comp > 0)
        {// t > node.data
            nodeParent = node;
            node = node.rightChild;
        }
        else
        {// t == node.data
            break;
        }
    }

    if (node == null)
    {// 没要找到要删除的节点
        return;
    }

    if (node.leftChild != null && node.rightChild != null)
    {// 左右子结点都存在
        BinaryTreeNode minNode = node.rightChild;
        BinaryTreeNode minNodeParent = node;
        while (minNode.leftChild != null &&
              comparer.Compare(minNode.leftChild.data, minNode.data) < 0)
        {
            minNodeParent = minNode;
            minNode = minNode.leftChild;
        }
        node.data = minNode.data;

        // 因为此时 minNode 的卫星数据已经替换了要删除的节点，相当于
        // 要删除的几点与 minNode 互换了位置，因此只需要删除 minNode 即可
        if (minNodeParent.leftChild == minNode) minNodeParent.leftChild = null;
        else minNodeParent.rightChild = null;
    }
    else
    {// 只有一个子结点，或者没有子结点
        BinaryTreeNode child = node.leftChild ?? node.rightChild;
        if (nodeParent == null)
        {// 要删除的为根节点
            tree = child;
        }
        else
        {
            if (nodeParent.leftChild == node)
            {
                nodeParent.leftChild = child;
            }
            else
            {
                nodeParent.rightChild = child;
            }
        }
    }
}

二叉搜索树的查找

在理解上面的插入和删除之后，查找就很容易实现了，不过需要注意的是，遍历的策略要和插入时一致，直接上代码：

public BinaryTreeNode FindNode(T t)
{
    BinaryTreeNode node = tree;
    while (node != null)
    {
        int comp = comparer.Compare(t, node.data);
        if (comp < 0)
        {
            node = node.leftChild;
        }
        else if (comp > 0)
        {
            node = node.rightChild;
        }
        else
        {
            return node;
        }
    }
    return null;
}

二叉搜索树与有序数组互转

将有序数组转为高度平衡二叉搜索树，高度平衡二叉搜索树左右子节点的高度相差不大于1，这里就不能使用上面的插入算法了，因为对于升序排列的数组，按照上面插入实现，结果必然是一个全为右子节点的链表。

具体实现思想是这样的，因为二叉树搜索树的每个节点都是它左右子树的中点，因此利用二分思想，不断的取出数组的中点，作为数的下一个节点，代码实现如下：

public TreeNode SortedArrayToBST(int[] nums)
{
    return SortedArrayToBST(nums,0,nums.Length-1);
}

private TreeNode SortedArrayToBST(int[] nums, int left, int right)
{
    if(left == right)
        return new TreeNode(nums[left]);
    else if(right < left)
        return null;

    int mid = left + (right - left) / 2;
    TreeNode node = new TreeNode(nums[mid]);
    node.left = SortedArrayToBST(nums, left, mid - 1);
    node.right = SortedArrayToBST(nums, mid + 1, right);
    return node;
}

将二叉搜索树转换为有序数组实现就相对简单一些，只需要中序遍历结点即可。

private static List<int> BSTToSortedArray(TreeNode node)
{
    List<int> list = new List<int>();
    InOrder(node,(n)=>list.Add(n.val));
    return list;
}

private static void InOrder(TreeNode node,Action<TreeNode> visitor)
{
    if(node == null) return;

    InOrder(node.left,visitor);

    if(visitor != null)
        visitor(node);

    InOrder(node.right,visitor);
}

二叉搜索树性能分析

随着新节点的插入，会形成各种形状的树，其中最极端的两种情况是：

最好情况是完全二叉树或满二叉树，此时搜索次数等于根节点的高度，时间复杂度为O(log(n))
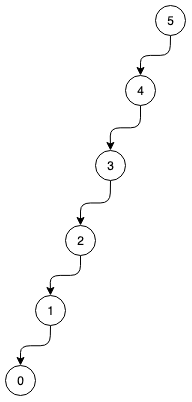
最坏情况是退化成链表，如下图所示，时间复杂度为O(n)

平衡二叉树

既然二叉树的插入、删除会造成二叉查找的退化，那么是否能够对二叉搜索树进行改进呢，因此就有了平衡二叉树，平衡二叉树需要保证随着插入、删除操作，都能够保持树的平衡，不会造成性能退化，能在O(logn)时间内完成插入、删除、查找操作，。平衡二叉树的形式多种多样，最早发明的平衡二叉树为 AVL 树，但目前用的最多的还是红黑树，C# 中的 SortedSet 类就是基于红黑树的有序列表。

平衡二叉树的严格定义是这样：对于树的任一节点，其左右子树的高度相差不超过1。

实际上很多平衡二叉树并不是严格遵循定义的，比如下面要介绍的红黑树，发明平衡二叉树的初衷是解决二叉搜索树退化问题的，因此只要能够保证时间复杂度不退化，就是满足需求的平衡二叉树。

2-3查找树

红黑树的原理理解起来不太容易，为了能够更好的理解红黑树，这里先介绍另一种平衡二叉树结构，叫做2-3树，在理解了2-3树的原理之后，就能够很容易红黑树了。

2-3查找树定义

一颗2-3查找树或者是一颗空树，或者包含如下节点：

2-节点：该节点内包含 1 个键值、2个子节点，左子树所有节点都小于该节点，右子树所有节点都大于该节点。（与二叉搜索树节点一致）
3-节点：该节点内包含 2 个键值、3个子节点，左子树所有节点都小于该节点，右子树所有节点都大于该节点，中子数所有节点的值都在 2 个键值之间。
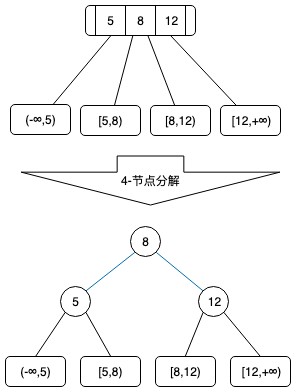
4-节点：该节点内包含 3 个键值、4个子节点，3个键值划分出4个区间，每个子节点对应一个区间，4-节点通常分解为2个2-节点，通过下图可以看出，4-节点分解之后，形成一个完全二叉树，并且根节点高度增长了1，2-3树就是通过这种方式来实现生长的。

下图是一颗2-3查找树：

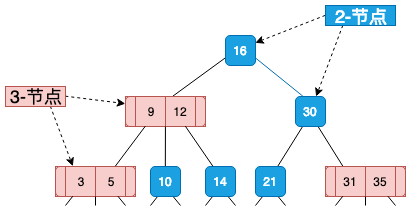
因为2-3查找树只是为了方便理解红黑树，所以这里只介绍它的相关原理，并不做具体的代码实现了。

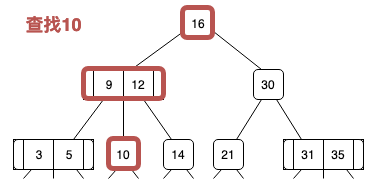
2-3查找树的查找

它的查找从根节点开始，按照如下过程进行查找：

与结点的键值对比，如果相等，则返回该节点
如果小于键值区间，则递归查找左子节点
如果处于键值区间，则递归查找中子节点
如果大于键值区间，则递归查找右子节点

2-3查找树的插入

因为2-3查找树要保持其平衡性，要比二叉搜索树插入复杂一些，流程大致如下：

首先找到新节点插入位置，这里和二叉搜索树类似，最终在树的底部找到插入的父节点，这个过程是自上而下的查找。
在找到父节点之后，根据父节点种类的不同，需要不同的插入方式。

根据父节点的种类，可以分为以下几种情况：

A:向2-节点插入，将2-节点转化为3-节点，并将新键保存到3-节点中
B:向3-节点插入，此时根据父节点类型不同，又分为三种情况：
- B1:没有父节点(为根节点)，将3-节点转换为4-节点(由2个2-节点表示)。
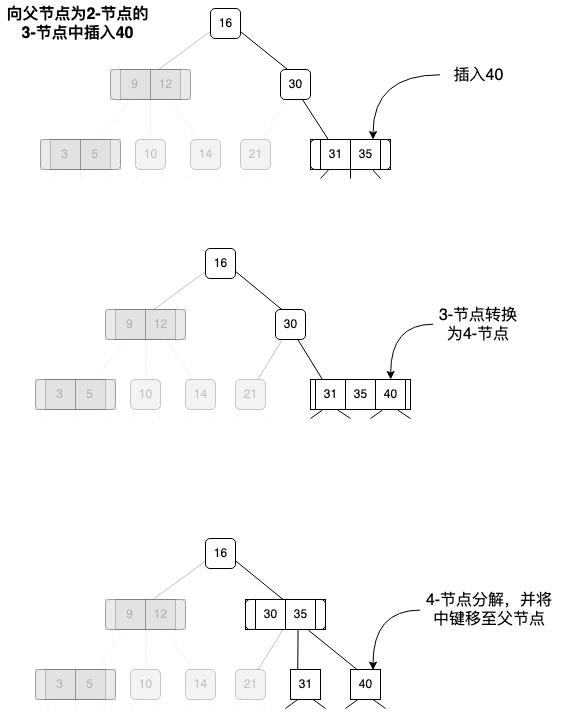
- B2:父节点为2-节点：将3-节点转换为4-节点，然后取出中键，将父节点转换成3-节点，该节点的中、右子树指向4-节点的左右子树（不存在中树了，因为中键取出了）。
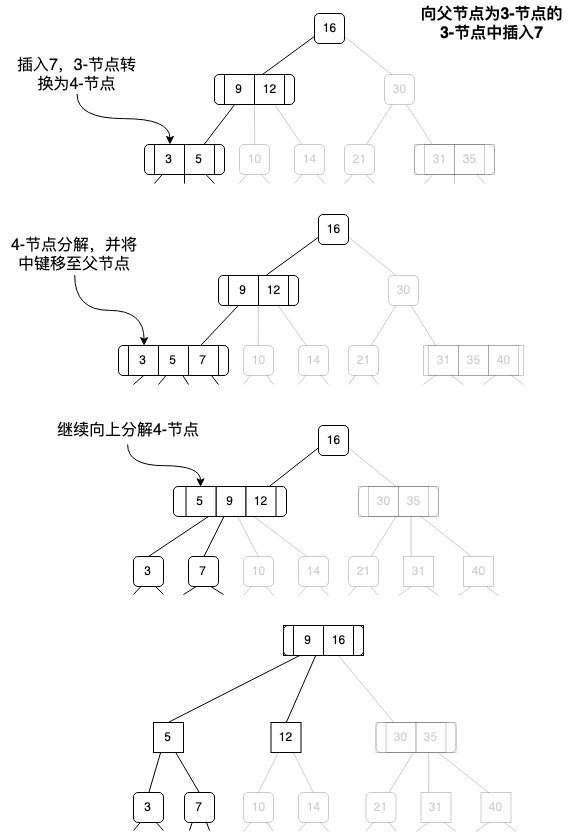
- B3:父节点为3-节点：
  1. 同样先将3-节点转换为4-节点并分解。
  2. 然后并将中键插入到父节点中，但是父节点也是3-节点，在对该父节点重复步骤1，直到父节点为2-节点，此时处理方式同 B2。
  3. 如果直到树的根节点都是3-节点，此时向根节点插入，处理方式同 B1。

向父节点为2-节点的3-节点中插入数据：

向父节点为3-节点的3-节点中插入数据：

2-3查找树的性能

2-3树性能主要体现在两点：

局部变换：将4-节点分解时，只影响其相邻的几个节点，而树的其他节点不需要做检查和调整。
全局特性：局部变换不会影响树的有序性和平衡性。
自平衡性：与二叉搜索树的自根向叶节点的生长不同，2-3树是自叶节点向根节点的生长，能够始终保持完美平衡。

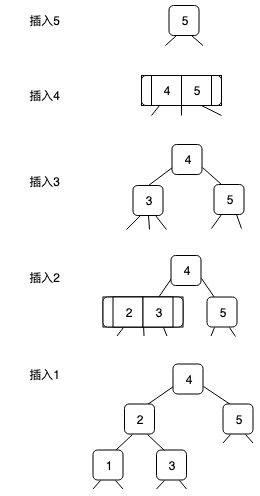
按照降序插入数据，在二叉搜索树中将会退化成链表，但是2-3树最终形成一颗完全二叉树。

其实在2-3树种进行插入、删除操作，能够始终保持完美平衡，因此，在一颗大小为 n 的2-3树种，查找和插入操作访问的节点个数必然不会超过$\lg{n}$个，即最坏情况的时间复杂度为$O(\lg{n})$。

2-3查找树的实现

既然2-3查找树能够实现完美平衡，那么为什么在实际中却很少使用过呢，原因主要有一下几方面：

需要维护多种节点类型，以及节点之间的转换、键值复制，会造成额外的性能开销，在节点较少时，性能可能比二叉搜索树还要慢。
实现不方便，需要处理的情况太多，代码不容易维护。

红黑树

在理解了2-3树的原理之后，再来理解红黑树就会容易很多，概括来说：红黑树是用标准二叉查找树（和颜色信息）来表示2-3树。为了实现这种表示，需要将2-3树的节点替换成二叉节点，2-节点不需要额外处理，因为它本身就是二叉节点，只需要对3-节点进行替换，替换方式是这样的：将3-节点表示为由一条左斜的红色链接相连的两个2-节点。

另外一种等价的定义是这样的：

红黑树是含有红黑链接，并满足以下条件的二叉查找树：

红链接均为左链接（右子节点不能为红链接）。
没有任何一个节点同时和两条红链接相连（节点与父节点链接、节点与左子节点链接，不能同时为红链接）。
该树是完美黑色平衡的，即任意叶子节点到根节点的路径上的黑链接数量相同。

满足这样定义的红黑树与2-3树是一一对应的（如果没有这些约束，3-节点就会有多种表示方式，一颗2-3树可能对应多种红黑树表示），对应转换关系如下图：

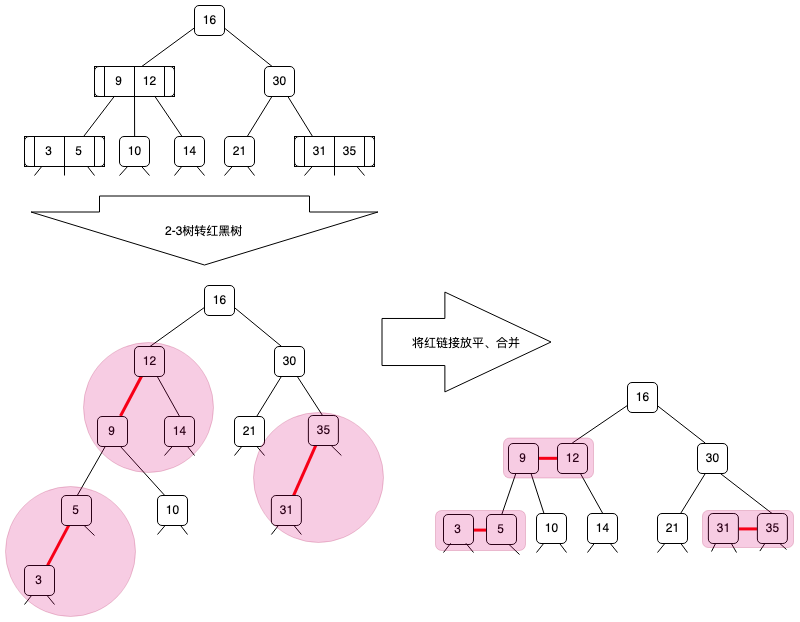
红黑树节点定义

因为每个节点只有一个父节点，因此可以将与父节点的链接颜色，存储到该节点当中，通过设置一个布尔值 isRed 指示节点与父节点链接的颜色，isRed = true 表示红链接，反之为黑链接，并且规定空链接为黑色（即根节点为黑色），节点定义如下：

public class RedBlackTree<T>
{
    public class Node
    {
        public bool IsRed;
        public Node Left;
        public Node Right;
        public T Item;
    }
}

红黑树的旋转

当红黑树进行插入、删除时，有可能遇到红色的右链接、两个连续的红链接等不符合红黑树约束的情况，此时就需要利用旋转进行维护，以保持其有序性和完美平衡性。通过下图和代码理解一下旋转的具体实现。（最好是自己能够画一下这个过程，加深理解）

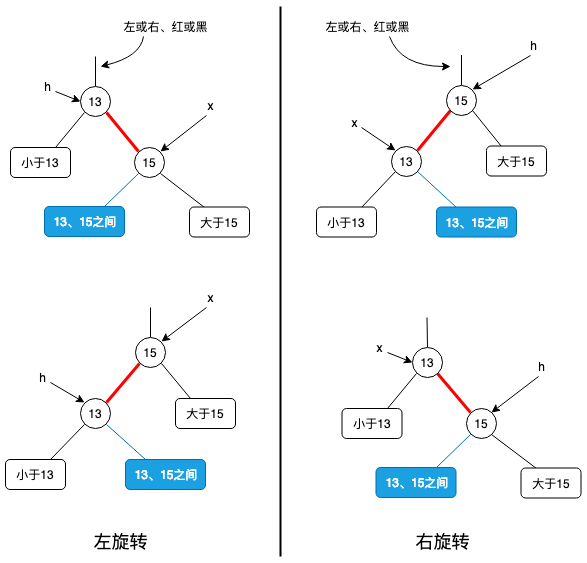
public Node RotateLeft(Node h)
{
    Node x = h.Right;
    h.Right = x.Left;
    x.Left = h;
    x.IsRed = h.IsRed;
    h.IsRed = true;
    return x;
}

public Node RotateRight(Node h)
{
    Node x = h.Left;
    h.Left = x.Right;
    x.Right = h;
    x.IsRed = h.IsRed;
    h.IsRed = true;
    return x;
}

红黑树的插入

用二叉搜索树的方式，向红黑树中插入新的键值，会在底部增加一个新的叶节点，并且新节点与父节点的链接总是红链接。红黑树和2-3树是一一对应的，插入可以原理也是相同的，只需要将2-3树的节点分解为红黑节点，就能完成红黑树的插入，下面按照2-3树的插入情形分类，来看看红黑树是如何与2-3树一一对应的。

A:向2-节点插入新键，将2-节点转换为3-节点。
- A1:如果插入到左子结点，不需要额外处理。
- A2:如果插入到右子节点，产生了红色右链接，所以需要坐旋转。
B:向3-节点插入新键，根据新键所在区间，分为以下三种情况
- B1:大于3-节点的两个键，插入到右子结点，插入之后形成左右两个红链接，此时需要将两个红链接变为黑色链接。
- B2:小于3-节点的两个键，插入到左子结点，插入之后形成两个连续红链接，此时只需右旋转即可得到 B1 情况。
- B3:介于两个键值之间，插入到中子结点，插入后形成两个连续红链接，一条红色左链接和一条红色右链接，此时只需左旋转红色右链接即可得到 B2 情况。

红黑树中向3-节点插入新键，与2-3树中3-节点插入新键的处理方式是类似的，最终都是形成一颗完全二叉树，只不过2-3树利用4-节点的分解来实现，而红黑树中采用旋转和颜色转换，虽然形式上略有区别，但是目的是一致的。

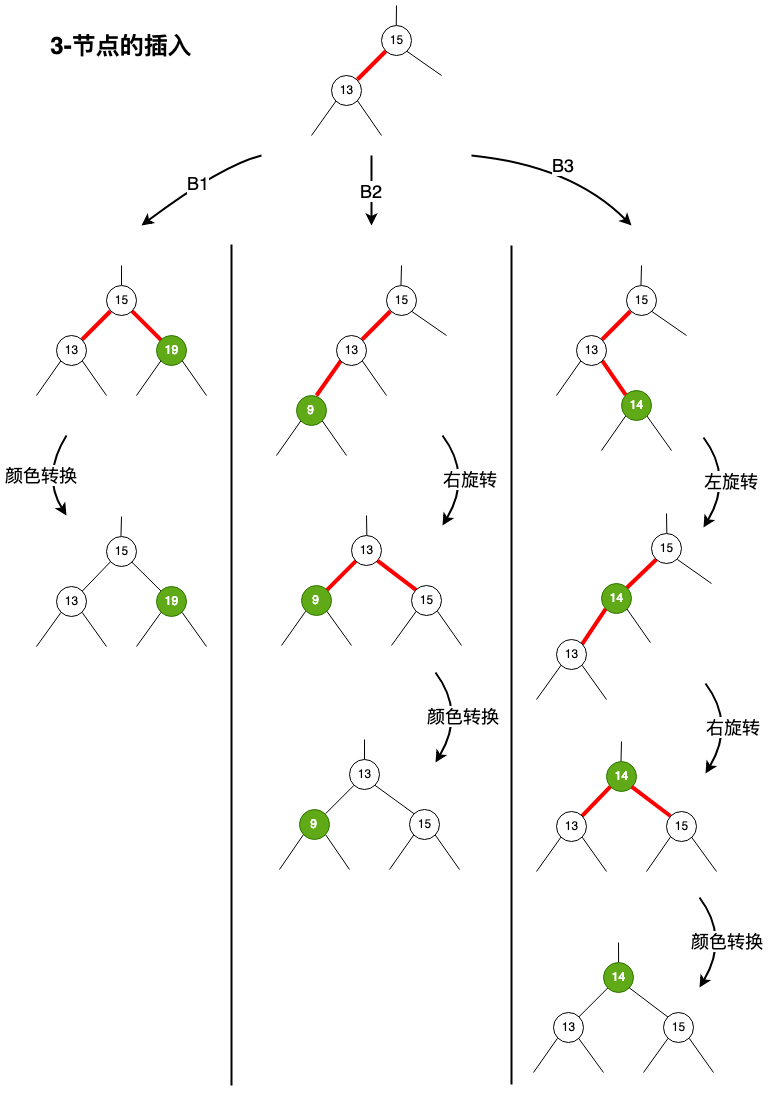
在上图中可以看到，最后一步处理都是颜色转换，需要将节点左右两个红链接转换为黑链接，同时还需要节点的与其父节点的链接转为红链接(这就等价于2-3树插入中，4-节点分解时，将上层2-节点转换为3-节点、3-节点转换为4节点)，代码如下：

public void FlipColor(Node h)
{
    h.IsRed = !h.IsRed;
    h.Left.IsRed = !h.Left.IsRed;
    h.Right.IsRed = !h.Right.IsRed;
}

既然颜色转换会修改父节点的链接颜色，那么就可能造成父节点不符合红黑树约束，因此需要继续向上转换父节点，所以这是一个从新插入节点到根节点的递归过程，对于每个节点，只要按照如下顺序进行检查，就能保证插入后与2-3树的一一对应关系(和2-3插入相同，都是自下而上分解4-节点的过程)：

右子节点为红色、左子结点为黑色，进行左旋转。
左子节点为红色、左子节点的左子节点也为红色，进行右旋转。
左子节点、右子节点都为红色，进行颜色转换。

为什么是这么一个检查顺序，其实这就是上面 B3 情况的处理流程，从“3-节点插入”图中可以看出，B1 是 B2 的子集、B2 是 B3 的子集，因此只需要按照 B3 的流程进行检查处理，就能够完成B1、B2 的检查处理。

最后，需要注意的是，在进行颜色转换时，对于根节点，要始终保持黑色，这是因为红链接表示3-节点的左子链接，而根节点没有父节点，所以不能表示为红链接。

以下是插入的实现代码：

public void Insert(T t)
{
   tree = InsertInternal(tree, t);
   tree.IsRed = false;
}

private Node InsertInternal(Node h, T t)
{
   if (h == null)
   {
       return new Node(t)
       {
           IsRed = true
       };
   }

   int comp = this.comparer.Compare(t, h.Item);
   if (comp < 0) h.Left = InsertInternal(h.Left, t);
   else if (comp > 0) h.Right = InsertInternal(h.Right, t);
   else h.Item = t;

   if (h.Right.IsRed && !h.Left.IsRed) h = RotateLeft(h);
   if (h.Left.IsRed && h.Left.Left.IsRed) h = RotateRight(h);
   if (h.Left.IsRed && h.Right.IsRed) FlipColor(h);

   return h;
}

红黑树的删除

虽然红黑树的插入已经很复杂了，但是红黑树的删除更加麻烦，因为它不仅需要在（为了删除结点而）构造临时4-节点时沿着查找路径向下进行变换，还要在分解遗留4-结点时沿着查找路径向上进行变换（同插入操作）。

下面先从比较简单删除最小值开始，一步步了解如何实现红黑树的删除操作。

删除最小值

因为最小值只可能在树的底部，并且是左链接，因此，先自上而下遍历初步调整左链接，这个过程是为了保证最终要删除的节点不是2-节点（2-节点删除会破坏整棵树的完美平衡性）；再自下而上的进行平衡调整。

首先是自上而下进行左子节点遍历，作用是将节点调整为非2-节点，可能会遇到以下几种情况：

在根节点：
1. 根节点及其左右子节点都是2-节点，合并为4-节点。
2. 否则需要保证根节点的左子节点不为2-节点，可以从右侧兄弟节点借一个键来。
其他非根节点：
1. 如果左子节点不是2-节点，不需要额外处理。
2. 如果左子节点是2-节点，且它的兄弟节点不是2-节点，将兄弟节点中的一个键移动到左子节点中。
3. 如果左子节点和兄弟节点都是2-节点，将左子节点、兄弟节点、父节点中的最小键合并为4-节点。

要将上述过程转换为代码，需要解决几个问题：

如何判断 h 节点的左子节点为2-节点
如何实现将 h 节点的左子节点的兄弟节点的一个键转移到左子节点中
如何将 h 节点的左子节点、兄弟节点、h节点中的最小键合并为4-节点

为了解决上面的问题，我们需要在回忆一下2-节点、3-节点、4-节点在红黑树中怎么表示，有一点需要注意，在下图中可以看到4-节点存在两个连续的红链接，这与红黑树的特性是违背的，但是因为这个4-节点只是临时存在，在进行自下而上的平衡调整时，就会消除这个问题，因此在转换4-节点是允许不满足红黑树特性的4-节点。

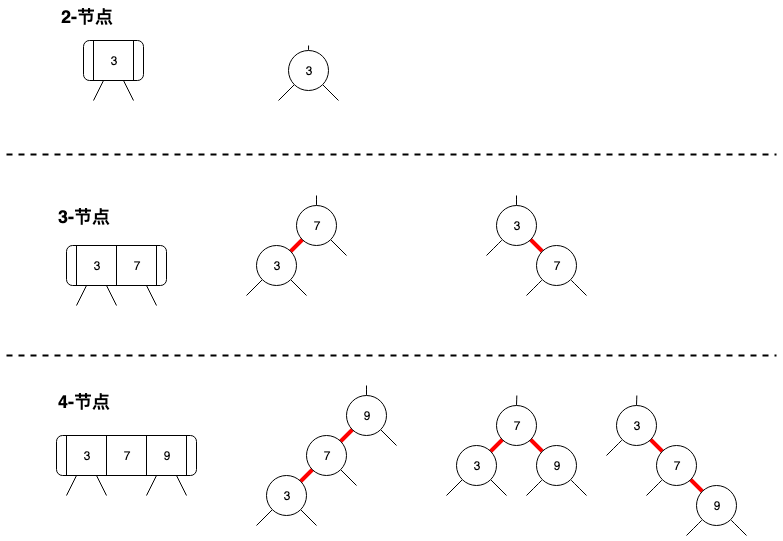
在清楚3-节点、4-节点如何表示之后，第一个问题就非常容易解决了，代码如下：

// 判断节点 h 的左子节点是否为2节点：
// 如果 左子链接为红链接，那么左子节点和 h 构成了 3-节点
// 如果 左孙子链接为红链接，那么左子节点和左孙子节点构成了 3-节点
// 如果 左子链接、左孙子链接都为红链接，那么 h节点、左子节点、左孙子节点构成了4-节点

// 因此节点 h 左子节点为2-节点的条件是：
if(!h.Left.IsRed && !h.Left.Left.IsRed)
{
    // h 左子节点为 2-节点
}

第二个问题解决起来比较麻烦，需要依次经过”颜色转换-右旋转右子节点-左旋转节点-颜色转换“，通过下面示例图来理解一下：

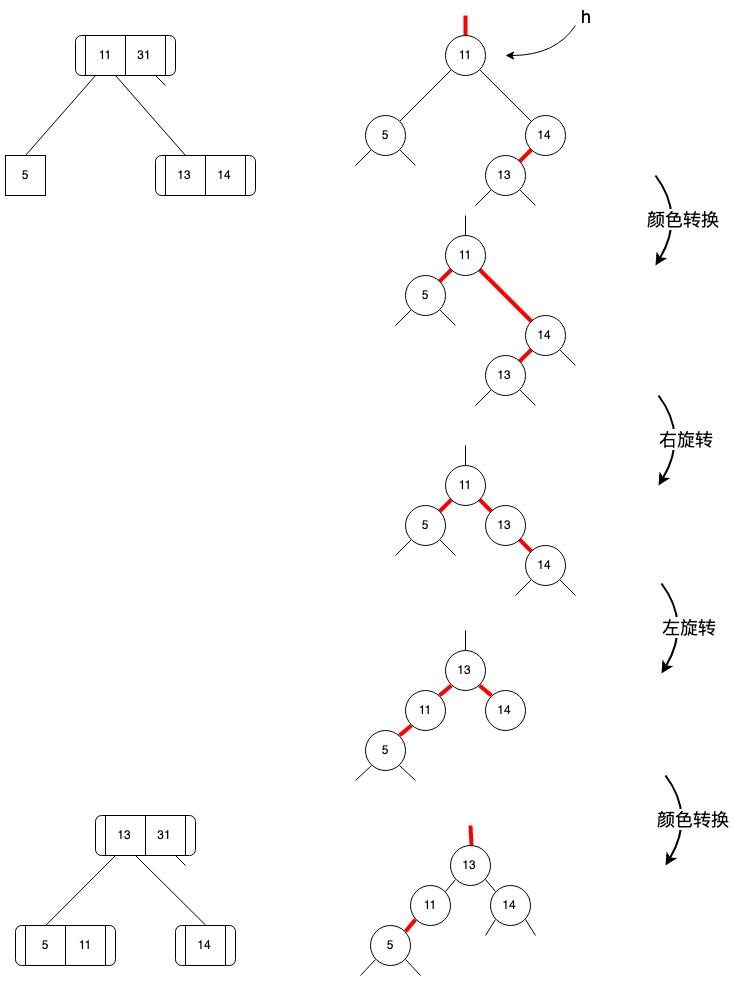
第三个问题稍微容易一些，因为自上向下处理过程中，能够确保 h 节点不是2-节点，因此解决问题3只需要将颜色进行转换，即可得到一个左右红链接的4-节点。这里需要再次强调一下，4-节点是自上而下调整过程中产生的临时节点，会在自下而上分解平衡的过程中进行消除，因此并不会影响红黑树的特性，合并过程如下图：

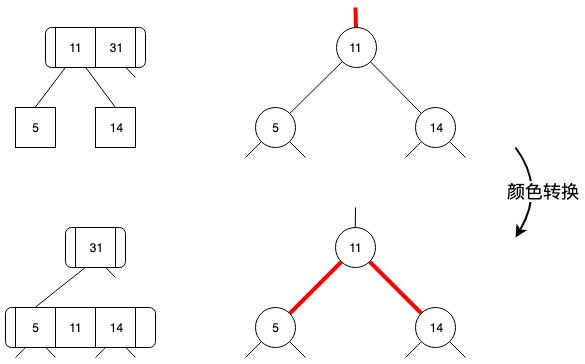
在解决了上面三个问题之后，代码实现起来就容易多了，直接上代码：

// 左子节点红链接 或 左孙子节点红链接表示3-节点
// 左子节点、左孙子节点都为红表示4-节点
// 左子节点、左孙子节点都不为红表示2-节点
if (!h.Left.IsRed && !h.Left.Left.IsRed)
{
    MoveRedToLeft(h);
}

private Node MoveRedToLeft(Node h)
{
   FlipColor(h);

   // 判断 h 右子节点是否为 3-节点 或 4-节点
   if (h.Right != null && h.Right.Left != null && h.Right.IsRed)
   {
       // 右子节点3-节点 或 4-节点，将右子节点的键移到左子节点中
       h.Right = RotateRight(h.Right);
       h = RotateLeft(h);
       FlipColor(h);
   }
   return h;
}

稍解释下上面代码，因为第二问题和第三个问题的解决方法，第一个步骤是相同的，区别部分在于右子节点非2-节点时，可以将右子节点的键转移到左子节点中，因此有了上面代码的第二个 if 判断。

在自上而下调整完毕之后，需要接着进行自下而上的分解调整时产生的4-节点，这里和插入时的分解4-节点非常类似，平衡代码如下：

private Node Blance(Node h)
{
   if (h.Right.IsRed) h = RotateLeft(h);
   if (h.Left.IsRed && h.Left.Left.IsRed) RotateRight(h);
   if (h.Left.IsRed && h.Right.IsRed) FlipColor(h);
   return h;
}

最后完整的删除最小值代码如下：

public void RemoveMin()
{
   if (tree == null)
       return;

   // 因为自上而下遍历过程中，能够保证左子节点非2-节
   // 因此左子节点与父节点的链接为红链接，为了递归中统一
   // 处理，如果根节点非2-节点，将根节点也设置为红色。
    if (!tree.Left.IsRed && !tree.Right.IsRed)
        tree.IsRed = true;

   tree = RemoveMinInternal(tree);
}

/// <summary>
/// 删除最小值的递归函数
/// </summary>
/// <returns>删除最小值后的左子树根</returns>
/// <param name="h">需要删除左子树中最小值的节点</param>
private Node RemoveMinInternal(Node h)
{
   if (h.Left == null)
       return null;

   // 左子节点红链接 或 左孙子节点红链接表示3-节点
   // 左子节点、左孙子节点都为红表示4-节点
   // 左子节点、左孙子节点都不为红表示2-节点
   if (!h.Left.IsRed && !h.Left.Left.IsRed)
   {
       h = MoveRedToLeft(h);
   }

   // 继续自上而下递归调整
   h.Left = RemoveMinInternal(h.Left);


   // 开始自下而上进行分解4-节点，平衡红黑树
   return Blance(h);
}

删除最大值

在理解最小值的删除之后，最大值的删除与之类似，同样首先需要自上而下的进行调整，然后再自下而上进行回溯，分解创建的4-节点，以保持红黑树的特性。

与删除最小值不同，因为最大值在底层的右子节点，所以需要保证右子节点不为2-节点，因此也会有以下几种情况：

如果节点的右子节点不为2-节点，则不需要额外处理。
如果节点的右子节点是2-节点，左子节点不是2-节点，则将左侧的键移到右子节点，构成3-节点
如果节点的在右子节点、左子节点都为2-节点，则将左子节点、右子节点、父节点组合成一个四节点。

第1、3和删除最小值类似，重点说一下第2种情况，在向下遍历路径上的节点 h 转换流程：“颜色转换-右旋转-颜色转换”，如下图所示：

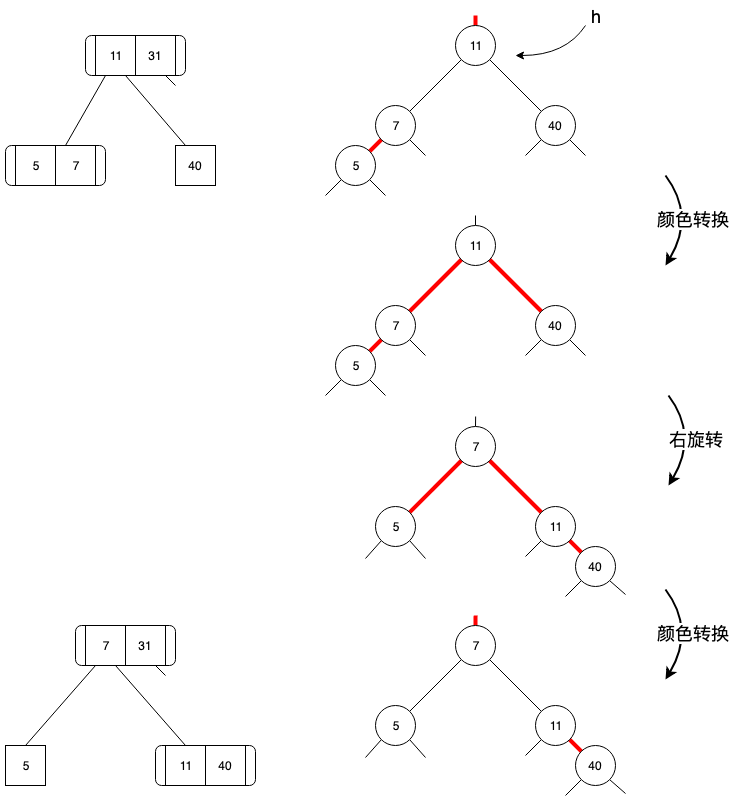
自下而上的消除4-节点的方式是相同的，直接给出删除最大值的代码：

public void RemoveMax()
{
   if (tree == null)
       return;

   if (!tree.Left.IsRed && !tree.Right.IsRed)
       tree.IsRed = true;

   tree = RemoveMaxInternal(tree);
}

private Node RemoveMaxInternal(Node h)
{
    // 因为左链接可以为红链接，所以可以直接将
    // 左链接的红链接旋转到右链接，使得右子节点变成3-节点或4-节点
    if (h.Left.IsRed)
       h = RotateRight(h);

    if (h.Right == null)
       return null;

    // 如果节点为2-节点
    if(!h.Left.IsRed && !h.Right.IsRed)
    {
       h = MoveRedToRight(h);
    }

    h.Right = RemoveMaxInternal(h.Right);

    return Blance(h);
}

private Node MoveRedToRight(Node h)
{
   FlipColor(h);

   // 判断左侧子节点是否非2-节点（3-节点、4-节点）
   if(h.Left != null && h.Left.Left != null && h.Left.Left.IsRed)
   {
       h = RotateRight(h);
       FlipColor(h);
   }
   return h;
}

删除任意值

在理解了最小值和最大值的删除之后，再来实现任意值得删除，就容易一些，方法与删除最大/最小值类似，同样需要先自上而下进行搜索调整，如果发现要删除的节点不在树底部，需要将要删除的节点和它左子树的最小节点进行交换（和二叉搜索树的删除相同），自上而下搜索完成之后，删除结点，然后自下而上地回溯搜索路径，将临时的4-节点进行分解，代码如下：

public void Remove(T t)
{
   if (t == null || !Contains(t))
       return;

   if (!IsRedNode(tree.Left) && !IsRedNode(tree.Right))
       tree.IsRed = true;

   tree = Remove(tree, t);

   if (tree != null)
       tree.IsRed = false;
}

private Node Remove(Node h, T t)
{
   if (comparer.Compare(h.Item, t) < 0)
   {
       if (!IsRedNode(h.Left) && !IsRedNode(h.Right))
           h = MoveRedToLeft(h);

       h.Left = Remove(h.Left, t);
   }
   else
   {
       if (IsRedNode(h.Left))
           h = RotateRight(h);

       if (comparer.Compare(h.Item, t) == 0 && h.Right == null)
           return null;

       if (!IsRedNode(h.Right) && !IsRedNode(h.Right.Left))
       {
           h = MoveRedToRight(h);
       }

       if (comparer.Compare(h.Item, t) == 0)
       {
           // 找到右子树的最小值，替换到要删除的节点
           Node x = MinNode(h.Right);
           h.Item = x.Item;

           // 替换完成之后，只需要将最小值节点删除即可
           h.Right = RemoveMinInternal(h.Right);
       }
       else
       {
           h.Right = Remove(h.Right, t);
       }
   }

   return Balance(h);
}

总结

红黑树之所以比较难学，个人认为主要原因在于它的旋转、颜色转换等操作的作用不够直观，并且这些操作会影响父子、兄弟节点，更是难以缕清之间的关系，所以将红黑树的操作和2-3树进行一一对应起来，便于学习和理解。

对于2-3树来说，3-节点、4-节点用红、黑链接有多种表示方式，因此红黑树规定了一些约束，这些约束一是保证一个2-3树只对应一种红黑树表示，另一个重要作用就是简化代码的实现。

最后附上完整代码。