数据结构与算法 - 跳表

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

数据结构与算法 - 跳表

在前面介绍了二分查找，它是一种时间复杂度为$O(\log{n})$的高效查询算法，因为它依赖于有序数组，因此存在一些局限性。我们知道链表不要求连续内存，但是它不支持随机访问，比如在链表 L 中，如果需要查找第 k 个元素，就需要从头开始挨个结点进行查找，那么应该如何提高这种有序链表查找效率呢，基于这个出发点，出现了跳表这种数据结构，

在介绍跳表之前，首先思考一下，对于一个有序链表，如何才能提高它的查找效率呢？

参考前面的二分查找思想，是不是同样可以将数据的中点提取出来，这样不就可以直接访问到中点了？至于结果行不行的通，先看下如果采用这种方法时的查找过程，见下图。

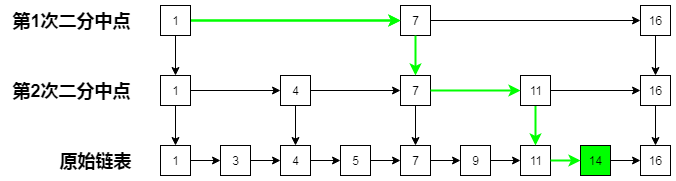
可以看出，如果我们挨个遍历的的话需要遍历8个元素，通过提取二分中点来查询则需要经过6个元素，虽然两者相差不多，但是对于规模非常大的数据来说，两者的差距也越大。

跳表是什么

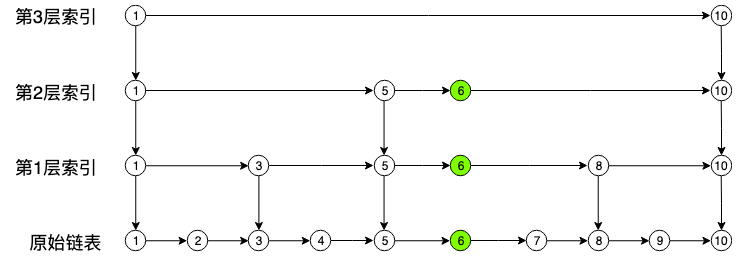
跳表的思想和上面所说的比较类似，都是通过提取多层索引来提高元素访问效率，但是跳表是通过间隔 n 个元素作提取，而非提取中间点，如下图：

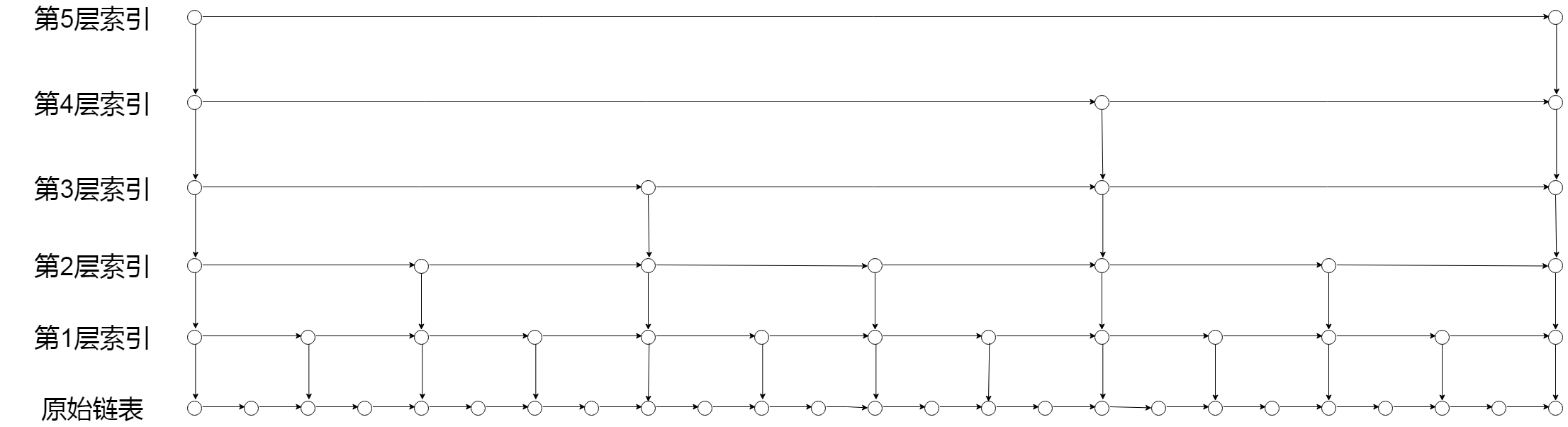
跳表的性能

首先分析跳表的查询的时间复杂度：

  1. 根据上图可以看出第1层索引的结点个数为 ${n}/{2^1}$，第2层结点个数为${n}/{2^2}$，依次类推第k层的结点个数为$n/{2^k}$。
  2. 假设跳表有 h 层索引，最高层只有首尾两个结点，即$n/{2^h}=2$，可以得到$h=\log_2{n}-1$，加上原链表本身一共 $\log_2{n}$ 层。
  3. 那么每层的复杂度是多少呢？即要遍历多少结点，因为经过上层的索引之后，就能够锁定查找的目标在下层的范围，所以每层最多遍历3个结点。
  4. 因此通过跳表查找元素的时间复杂度为：$T(n)= O(3\log_2{n}) = O(\log_2{n})$。

跳表的空间复杂度：

通过上面计算，知道第k层的节点个数为$n/{2^k}$，根据下面的几何级数求和公式，(h=$\log_2n-1$)可以计算出总结点个数为：n-2，因此跳表的空间复杂度为O(n)。

这里需要强调的是，虽然空间复杂度为O（n），但是索引结点只存储结点指针，并不存储数据内容，在实际开发中，链表存储的数据内容通常是非常大的，此时就不必太强调空间复杂度。

跳表的实现

与链表不同，跳表的节点还需要存储它的索引信息，下面是节点类设计：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
// 跳表类型
public class SkipList<T>
    where T: IComparable<T>
{
    // 头结点
    private SkipListNode head;

    // 尾节点
    private SkipListNode tail;

    // 最大层数
    private int levelCount;

    // 跳表节点
    public class SkipListNode
    {
        // 节点包含的层
        public SkipLevel[] levels;

        // 后退节点
        public SkipListNode backward;

        // 节点数据
        public T item;
    }

    // 跳转层
    public class SkipLevel
    {
        // 前进节点
        public SkipListNode forward;
    }
}

SkipList 表示跳表数据类型，包含头结点引用和尾节点引用。
SkipListNode 表示链表的节点，每个节点都可能包含多层索引和后退节点，索引用 SkipLevel 表示，其中 forward 表示节点在该层跳转的节点，可以通过下图来帮助理解。

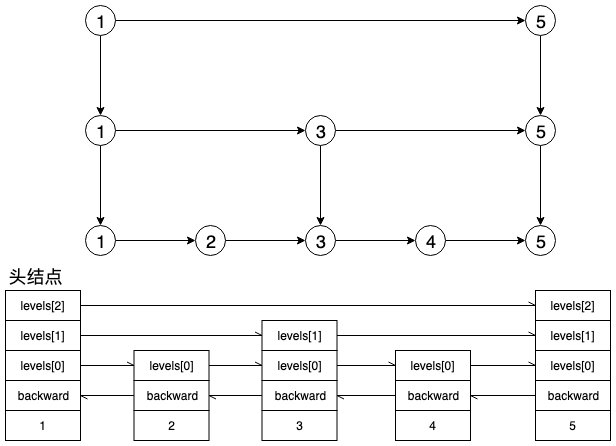
查找操作

查找应该从头结点的最顶层索引开始，递归的遍历前进节点，因为跳表的元素都是有序排序的，所以当节点的前进节点大于要查找的元素时，就需要进入下层索引进行查找，当所有层都遍历完成之后，得到了一个边界节点，需要进一步比较确认，它的前进节点是不是要查找的元素，详细代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 查找指定节点
public SkipListNode FindNode(T target)
{
   // 从头结点开始
   var node = head;

   // 从最顶层索引开始查找
   for (int i = levelCount - 1; i >= 0; i--)
   {
       while (node.levels[i] != null && node.levels[i].forward.item.CompareTo(target)<0)
       {
           // 跳转到该层的前进节点
           node = node.levels[i].forward;
       }
   }

   // 循环退出，说明 node 的下一个节点，要么大于查找目标，要么等于查找目标

   // 进一步判断是否为查找目标
   if (node.levels[0] != null && node.levels[0].forward.item.CompareTo(target) == 0)
   {
       return node.levels[0].forward;
   }
   else
   {
       return null;
   }
}

插入操作

向跳表中插入元素时，必须同时更新索引，如果不更新，就可能造成两个索引节点之间节点过多，查询时间复杂度也会退化为O(n)。

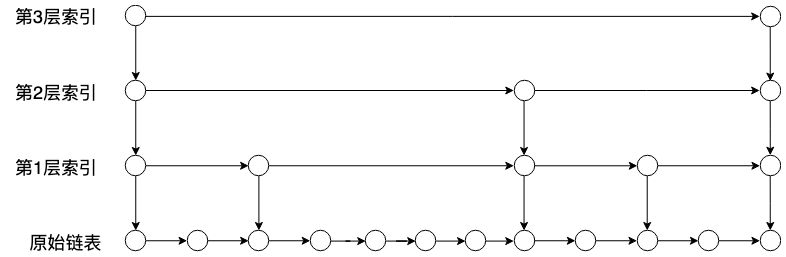
为了解决该问题，最直接的办法就是每次插入新元素之后，把插入位置之后的索引重新进行计算，但是这样在效率上就会比较低。有一种比较折中的办法，既能够很大程度的降低跳表退化概率，同时在插入效率上也比较高，该方法是在插入时，随机的选取一个层，在该层和之下层中插入索引结点。

结合上图理解一下跳表的插入步骤：

  1. 随机选取层索引，下面更新选取层和其下的所有层，上面是[0,2]。
  2. 找到各层需要插入的位置，上面各层都是结点5。
  3. 更新各层的索引的前进结点，在上图中，是将各层结点5的前进结点指向新结点6，将6的前进节点指向结点5之前的前进结点。
  4. 更新后退结点。

结点属性的变化关系如下图：

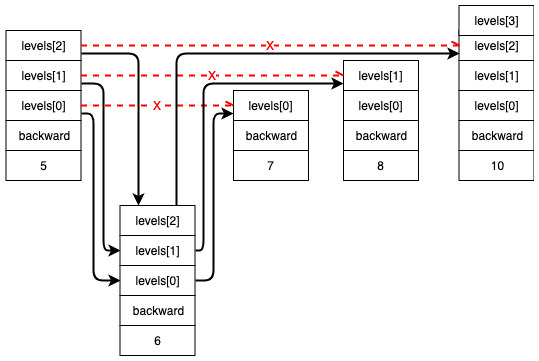
代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
public void Insert(T t)
{
   // 获取随机索引层[1,MAX_LEVEL_COUNT]
   int level = RandomLevel();

   // 创建新节点
   SkipListNode node = new SkipListNode();
   node.backward = head;
   node.levels = new SkipLevel[level];
   node.item = t;

   // 在每层中，找到要插入的位置（临界结点），
   // 并且暂时借用新节点的levels,将找到的节点存到其中
   SkipListNode temp = head;
   for (int i = level-1; i >= 0; i--)
   {
       node.levels[i] = new SkipLevel();
       while (temp != null && temp.levels!= null &&
              temp.levels[i] != null && 
              temp.levels[i].forward != null && 
              temp.levels[i].forward.item.CompareTo(t) < 0)
       {
           temp = temp.levels[i].forward;
       }
       node.levels[i].forward = temp;
   }

   // 然后设置临界结点和新结点的前进结点和后退节点
   for (int i = 0; i < level;i++)
   {
       // 要插入的临界结点
       var bound = node.levels[i].forward;
       temp = bound.levels[i].forward;

       // 设置前进结点
       bound.levels[i].forward = node;
       node.levels[i].forward = temp;

       // 设置后退结点
       node.backward = bound;

       if(temp != null)
       {
           temp.backward = node;
       }
   }

   if(node.levels[0].forward == null)
   {
       tail = node;
   }
}

在选择索引层时使用了随机算法，为了保证随机结果能够均匀分布，将随机算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
private int RandomLevel()
{
   int level = 1;
   for (int i = 0; i < MAXLEVELCOUNT; i++)
   {
       if (this.random.Next() % 2 == 0)
       {
           level++;
       }
   }

   return level;
}

删除操作

在理解了跳表的插入过程之后，删除操作也就很好理解了，除了要删除源链表的结点之外，还要删除该节点对应的索引节点，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public void Remove(T t)
{
   SkipListNode[] needUpdates = new SkipListNode[this.levelCount];
   SkipListNode temp = this.head;

   // 查找边界点:
   // A[i] < t,A[i+1]>= t，即找到A[i]之后
   // 需要进一步判断就是否为要删除的值
   for (int i = this.levelCount - 1; i >= 0; i--)
   {
       while (temp != null && temp.GetForward(i) != null && temp.GetForward(i).item.CompareTo(t) < 0)
       {
           temp = temp.levels[i].forward;
       }

       needUpdates[i] = temp;
   }

   // 源链表中的节点，如果该值与要删除的不相等，说明要删除的元素在跳表中不存在
   var node = temp.GetForward(0);
   if (node != null && node.item.CompareTo(t) == 0)
   {
       // A->B->C，更新为：A->C，其中B为要删除的结点
       for (int i = 0; i < this.levelCount; i++)
       {
           SkipListNode forward = needUpdates[i].levels[i].forward;
           if (forward.item.CompareTo(t) == 0)
           {
               needUpdates[i].levels[i].forward = forward.levels[i].forward;
           }
       }
   }
}

最后

上面介绍了跳表一些常用操作和实现，相对于之后要介绍的二叉平衡树要简单，在查询、插入等操作上效率也非常高。在开源K-V
数据库 Redis 中就使用了跳表，感兴趣的可以学习一下，最后完整的代码在这里。