数据结构与算法 - 排序算法(上)

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

在游戏开发中，经常会用到排序算法，比如背包物品排序、排行榜排序等等。本节主要介绍几种排序算法，包括冒泡排序、插入排序、选择排序，快速排序、归并排序、桶排序、基数排序，对于这些排序算法，在平时使用中，应该如何选择呢？或者说应该从哪些方面对比这些算法，通常包括以下几方面：

  • 时间复杂度
  • 空间复杂度（主要比较是否原址排序）
  • 是否稳定

在开始正式介绍之前，先把问题和输入描述一下：

将一个数组按照从小到大进行排序。
输入：一个包含 n 个元素的数组 v。
输出：将数组 v 按照从小到大重排。

然后在安利一个算法可视化网站，这里可以看到各种排序算法执行过程。

选择排序

选择排序应该算是最简单的一种排序算法了，它的规则是这样：将待排序数据分为已排序和未排序两部分，每次遍历，从数组中找到最小的元素，将它与待排序区第一个元素进行位置交换；剩下的数组还未排序，接着用同样的方法处理剩下的元素，直到整个元素都是有序的。

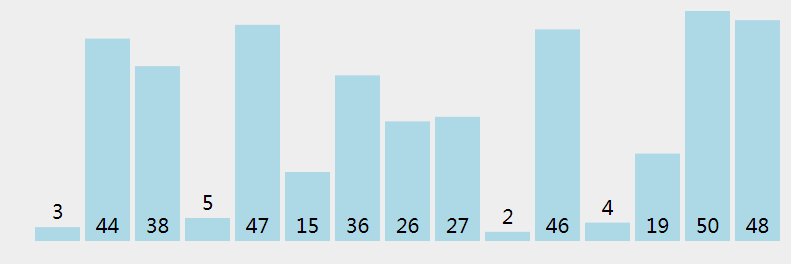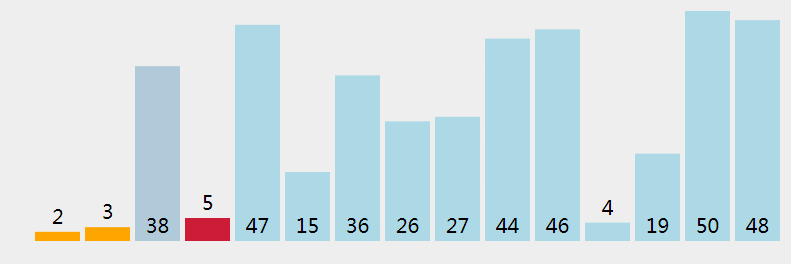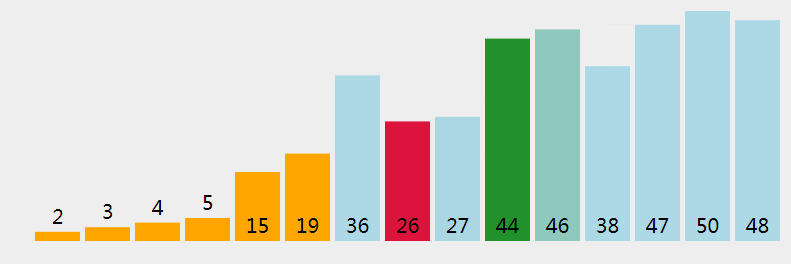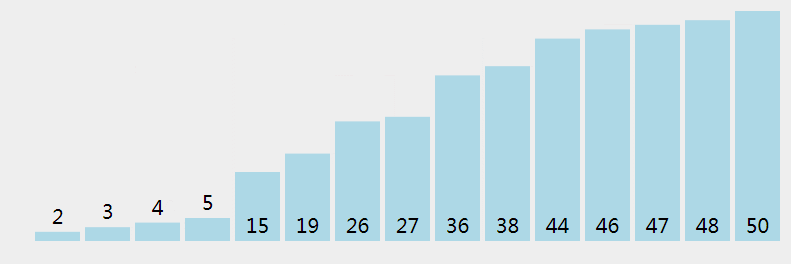
从问题中，很明显的看出数据规模在不断减小，应该能够很容易的写出它的递归式：

具体实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
function FindMinAndSwap(v, s)
    -- 存储最小值索引
    local minIndex = s

    for i = s, #v do
        if v[i] < v[minIndex] then
            minIndex = i
        end
    end

    -- 交换
    v[s], v[minIndex] = v[minIndex], v[s]
end

function SelectSort(v, s)
    if s <= #v then
        -- 找到最小值并交换
        FindMinAndSwap(v, s)

        SelectSort(v, s + 1)
    end
end

非递归形式：

1
2
3
4
5
6
7
8
9
10
11
function SelectSortNoRecursion(v)
    for i = 1, #v do
        local minIndex = i
        for j = i, #v do
            if v[j] < v[minIndex] then
                minIndex = j
            end
        end
        v[i], v[minIndex] = v[minIndex], v[i]
    end
end

下面分析一下它的复杂度：

  • 选择排序是一种不稳定排序，因为每次排序都要将最小元素和未排序首元素进行交换。
  • 空间复杂度，因为是原址排序，所以空间复杂度为 O(1)。
  • 时间复杂度，因为包含嵌套循环，并且内存循环规模在不断减小，中间不涉及跳出循环，所以最好情况、最坏情况、平均情况都相同，可以很容易得到时间复杂度为：

冒泡排序

冒泡排序的思想也比较简单，冒泡排序也是将带排序的数据分为已排序和未排序两个区，每次遍历未排序区，将最大的元素交换到未排序区末尾（排序区头），冒泡排序只进行相邻元素的比较，如果相邻元素不满足排序规则，就交换位置，遍历完之后，最大元素就被交换到了末尾。文字描述不够直观，看下面动画。

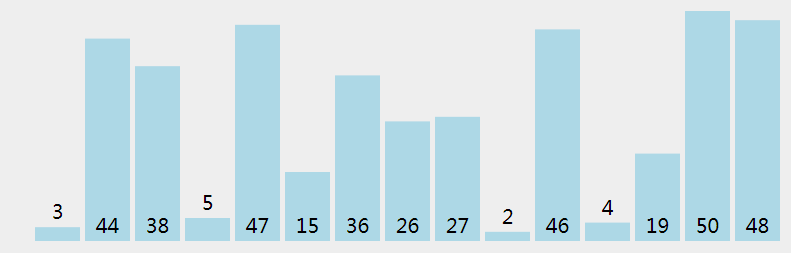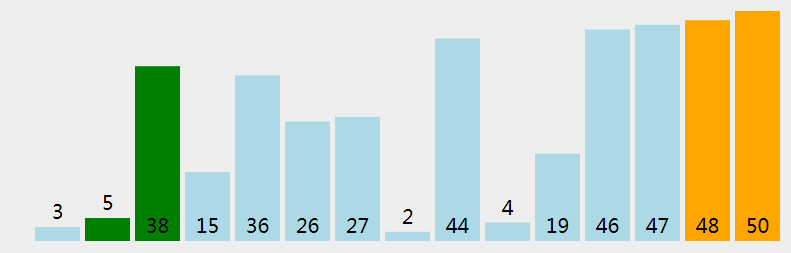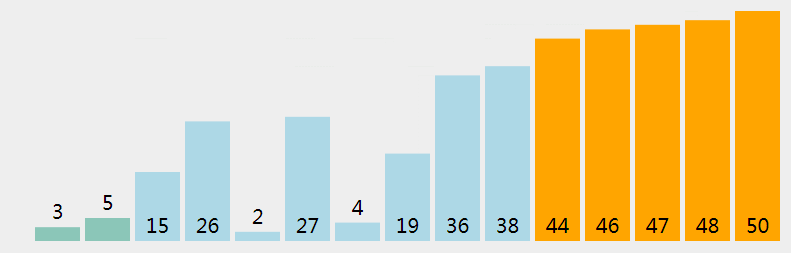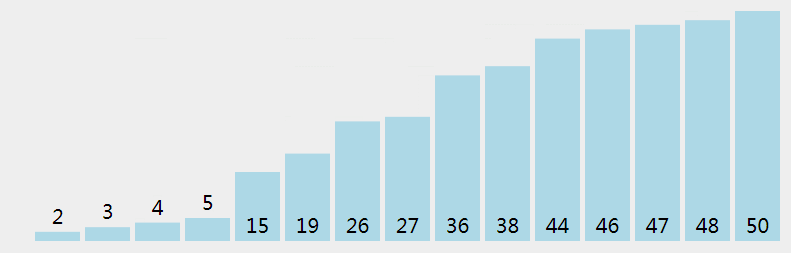
递归式表示 (e 表示未排序区尾端索引)：

根据递归式转换成Lua代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
-- 一次冒泡
function bub(t,e)
  if e < 2 then
    return
  end
  
  for i = 1,e-1 do
    if t[i] > t[i+1] then
      t[i],t[i+1] = t[i+1],t[i]
    end
  end
end

-- 冒泡排序
function bub_sort(t,e)
    if e < 2 then
      return
    end

    bub(t,e)

    bub_sort(t,e-1)
end

上面代码是写完了，但是还可以在进行优化，首先看一下上面冒泡函数的意义，它是把最大的元素通过不断的位置交换，最终交换到数组尾部，但是如果没有发生交换呢？不就说明每个元素与后一个元素都满足排序要求，即已经是有序的了，因此如果在一次冒泡中，如果没有发生位置交换，则说明未排序区元素已经有序，排序完成了，下面用非递归再实现一下。

非递归形式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function bub_sort_norecu(t)
  -- 每次冒泡，未排序区都在减小
  for i = #t,2,-1 do
    -- 记录一次冒泡过程中，是否发生了位置交换
    local swap = false

    -- 冒泡：从未排序头->未排序尾元素
    for j = 1,i do
      if j < i and t[j] > t[j+1] then
        t[j],t[j+1] = t[j+1],t[j]
        swap = true
      end
    end

    if not swap then
      break
    end
  end
end

最好情况渐进时间复杂度为：$O(n)$，最坏情况为：$O(n^2)$，平均情况时间复杂度为：$O(n^2)$，计算过程比较麻烦，下面详细解释一下。

逆序对：在集合A中，i<j并且A[i]>A[j]，则称A[i]、A[j]为逆序对；反之称之为有序对。

对于一个包含 n 个元素的数组，从中任意取出2个元素（前后顺序不能变），一共有$C_n^2$种取法，这两个元素不是有序对就是逆序对，因此：

例如：数组<2,3,8,6,1>的逆序对为：<2,1> <3,1> <8,1> <8,6> <6,1>共5个逆序对。
再例如：对于完全有序的数组<1,2,3,4,5,6>，从其中任取两个元素都是有序对，因此有序对个数为：$C_6^2=15$，逆序对个数为：0。
排序的过程就是减少逆序对，增加有序对的过程，当逆序对个数为0时，说明排序完毕。

还是回到冒泡排序的平均情况复杂度分析，最好情况是完全有序，即逆序对个数为0；最坏情况为完全逆序，逆序对个数为：$C_n^2$，即需要进行$C_n^2$次位置交换；此时我们可以简单的认为平均情况下需要进行$(0+C_n^2)/2$次交换，因此平均情况时间复杂度为：

插入排序

插入排序的基本思想是：将数据分为未排序和已排序两个区，已排序区在未排序区之前，将未排序区的元素依次取出，然后插入到已排序区中。

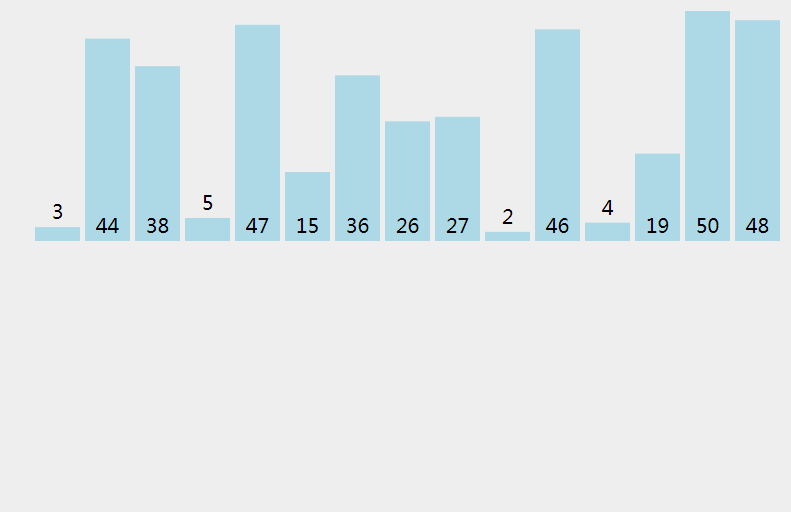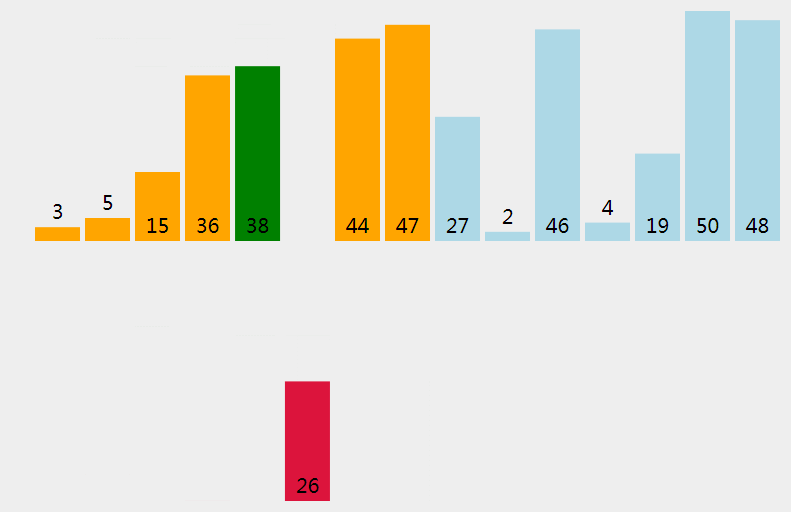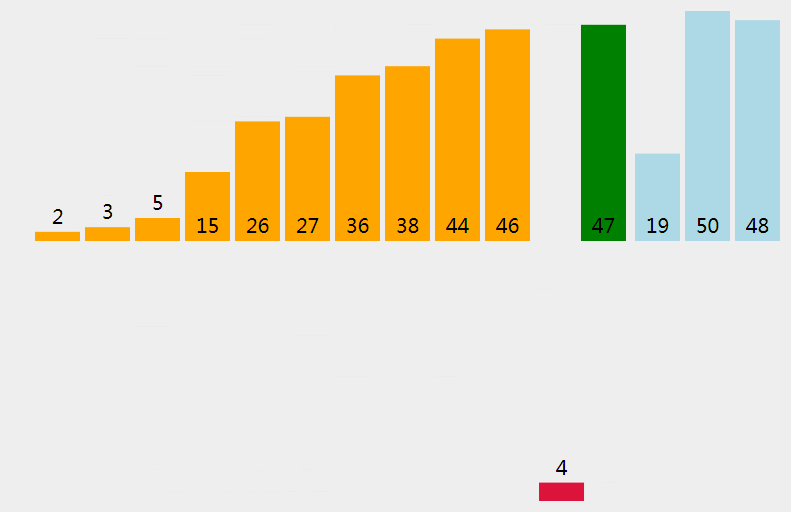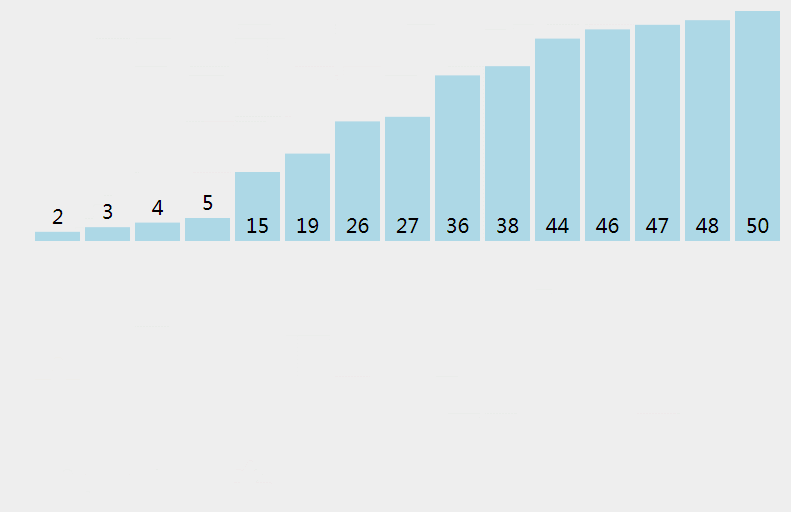
按照分治策略解决该问题，也比较简单，这里直接上递归式，其中 e 表示w未排序去头端索引：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public void InsertSort(int[] arr)
{
    for (int i = 1; i < arr.Length; ++i)
    {
        int val = arr[i];
        int j = i - 1;
        for (; j >= 0; --j)
        {
            if (arr[j] > val)
                arr[j + 1] = arr[j];
            else
            {
                break;
            }
        }
        arr[j + 1] = val;
    }
}

再来分析一下插入排序的复杂度：

插入排序是一种稳定的算法
插入排序为原址排序，所以空间复杂度为：$O(1)$
最好情况复杂度：输入的数据完全有序，此时只需要$O(n)$的复杂度
最坏情况复杂度：输入的数据完全逆序，此时的复杂度为：$O(n^2)$
平均情况复杂度：还是利用上面逆序对来计算，最好情况逆序对为0,最怀情况的逆序对为$C_n^2$，平均情况的逆序对为$C_n^2 / 2$，因此平均情况时间复杂度为：$O(n^2)$

总结

到目前为止，介绍了选择排序、冒泡排序、插入排序，细心的可能已经发现，这三种排序算法都是将集合分为两个区：已排序区、未排序区，不同的地方在于，将未排序元素转换到已排序区中，下面通过一个表格再来总结一下。

算法 是否稳定 最好情况 最坏情况 平均情况 空间复杂度 区别
选择排序 否 $O(n^2)$ $O(n^2)$ $O(n^2)$ $O(1)$ 找到最小，放到队头
冒泡排序 是 $O(n)$ $O(n^2)$ $O(n^2)$ $O(1)$ 从头到尾，遇大则交换
插入排序 是 $O(n)$ $O(n^2)$ $O(n^2)$ $O(1)$ 未排序头元素，从已排序尾向头作比较，将待排元素插入