数据结构与算法 - 有根树的表示

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

数据结构与算法 - 有根树的表示

前面介绍了链表、队列、栈，它们都是线性数据结构，下面介绍另一种形式的结构-树形结构，它的应用非常广泛，比如堆排序、二叉搜索、A*算法等等，本文不会介绍关于这些算法的东西，主要学习一下有根树相关的一些概念、表示方法，以及一些常用操作的实现。

概念

什么是树？现实中的树是一个主干，主干上分出很多的枝干，枝干再进分，最后是树叶。有根树与这种结构非常相似，如下图所示。

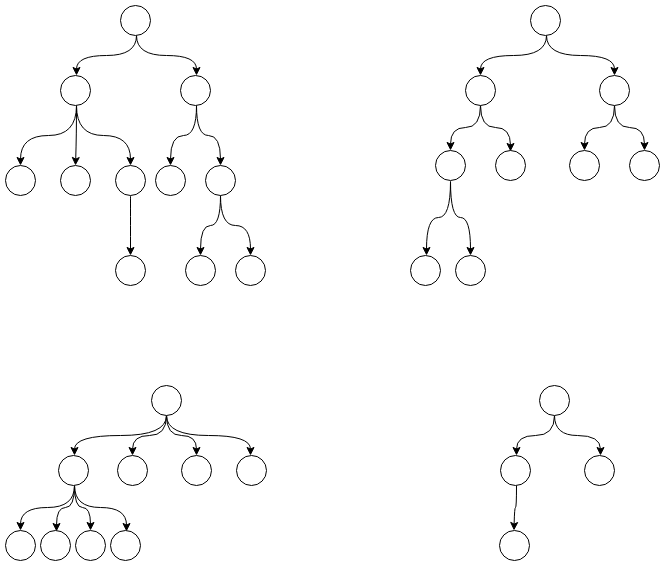
可以看出，树是由一个个结点组成的，结点之间通过线连接，形成一种父子关系，每个结点可以有多个子结点，但是只能有一个父结点，其中有两种比较特殊的结点：

  • 根结点：没有父结点的结点
  • 叶子结点：没有子结点的结点

关于结点还有几个相关概念：深度、高度、层数。

  • 深度：根结点到结点所经历的边数
  • 高度：从最底层叶子结点到结点所经历的边数
  • 层数：结点的深度 + 1
  • 树的高度 = 根结点的高度

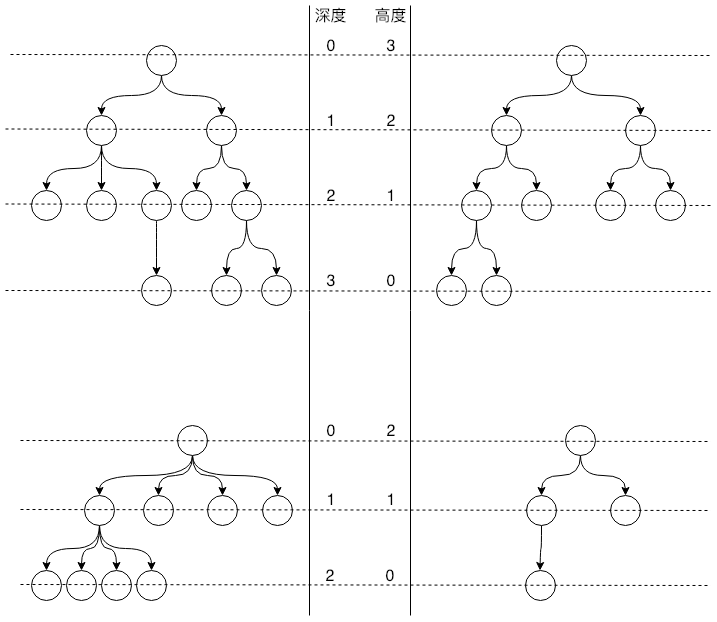
关于区分高度和深度有个小窍门，我们平时说高度，比如楼高，都是从底层地面往上数，树的高度也是从最底层往上数；一般说深度，比如水井深度，都是从最顶层往下数，树的深度也是从最顶层往下数。

二叉树：树的每个结点最多有两个子结点

完全二叉树：树的叶子结点都在最底下两层，最后一层的叶子结点都靠左排列，并且除了最后一层，其它层的子结点数量到达最大。（整个树按照从左到右、从上到下遍历过去，中间不能出现空洞，这种完全二叉树适合使用数组进行存储）。

满二叉树：完全二叉树的进化体，树的叶子结点都在最底层，除了叶子结点，其他结点的子结点数量都达到最大个数。

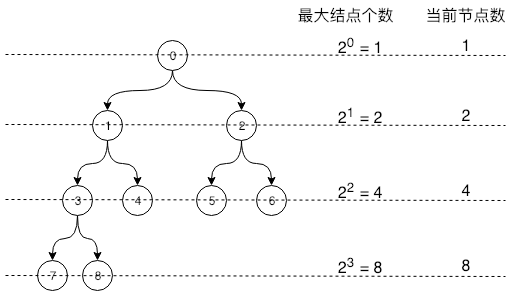
一个包含 n 个元素的完全二叉树，对于任意编号为 i 的元素，具备如下性质：

  • 当 i = 0 时，该元素为二叉树的根；i > 0 时，其父结点编号为 $i/2-1$。
  • i 结点的左子结点如果存在，则索引为 $2i+1$。
  • i 结点的右子结点如果存在，则索引为 $2i+2$。

树的表示法

左右孩子表示法

根据不同的需求，树可以有不同的表示方法，对于子结点数量确定的树，如二叉树（最多两个子结点）、四叉树、八叉树，可以使用“父-子”关系表示，即父结点下面连接的结点都是该结点的子结点，大概的结点数据结构类似下面：

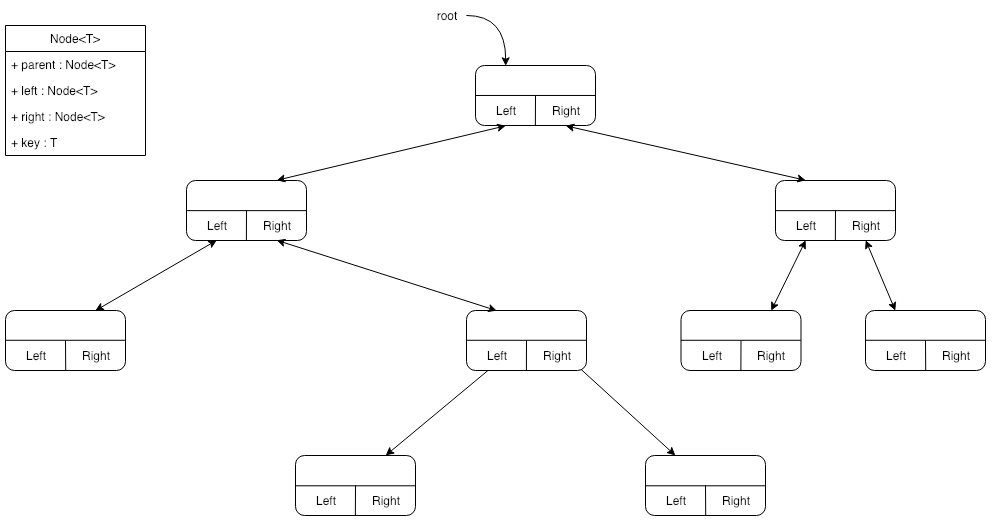
左孩子右兄弟表示法

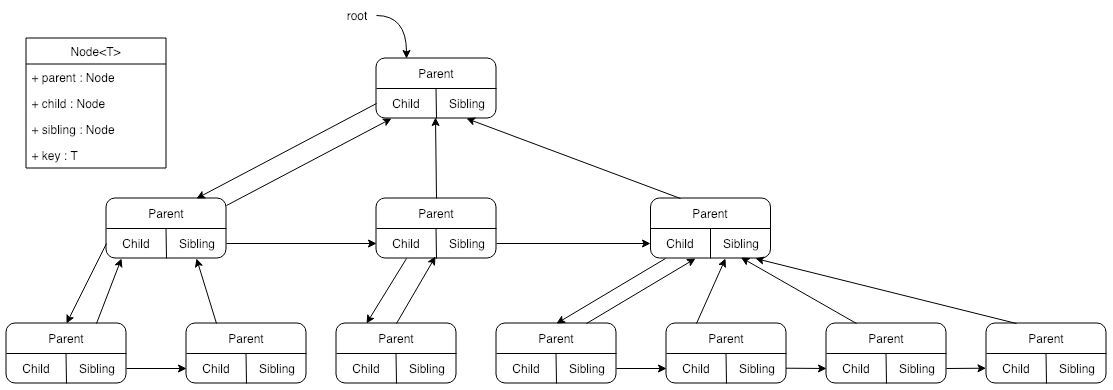
但是对于子结点数量不确定的树，上面这种表示方法就不太适用了，即使采用一个数组来存储子结点，也有可能造成内存上的浪费。这种情况，可以采用一种叫做“左孩子右兄弟”的表示法，这种表示法中，每个结点都有两个指针：

  • 一个指向该结点最左侧的孩子结点
  • 一个指向该结点右侧的兄弟结点

树的遍历

在介绍树的遍历之前，不妨根据之前所学的分治策略，来分析一下如何遍历一个树。

  1. 分解问题，主问题是要遍历根结点以及它所有的子结点、孙子结点等等，可以将问题分解成：
    • 处理根结点
    • 遍历左子结点
    • 遍历右子结点
      其中后两个子问题和主问题是相同的，所以可以使用递归。
  2. 解决问题，递归什么时候终止呢？如果不能存在左子结点/右子结点时，就应该停止递归。
  3. 合并结果。

可以写出它的递归公式：

在解决子问题时，根据处理根结点的时序不同，可以分为前序遍历、中序遍历、后序遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//前序遍历
template <class T>
void preOrder(binaryTreeNode<T> *t){
    if(t!= NULL){
      visit(t);
      preOrder(t->leftChild);
      preOrder(t->rightChild);
    }
}

//中序遍历
template <class T>
void inOrder(binaryTreeNode<T> *t){
    if(t!= NULL){
      inOrder(t->leftChild);
      visit(t);
      inOrder(t->rightChild);
    }
}

//后序遍历
template <class T>
void postOrder(binaryTreeNode<T> *t){
    if(t!= NULL){
      postOrder(t->leftChild);
      postOrder(t->rightChild);
      visit(t);
    }
}