数据结构与算法 - 分治策略

前面介绍了一些复杂度分析方法，以及一些基础的数据结构，后续将会开始介绍一些常见算法和一些高级的数据结构，在介绍这些内容之前呢，首先需要先了解一下分治策略，分治策略只是为解决某些问题提供了指导思想，真正落到编码上的，其实是递归方法，因此可以认为递归是分治策略的一种实现手段。

考虑这么一个情景，小A去电影院看电影，入座之后，小A想知道自己是第几排，但是灯光比较暗，不好一排排数，小A就问他前排，心想如果知道前排是第几，就能知道自己排数了。但是前排同样也不知道，他也问前一排，就这样一直问道第一排，它回复后面说自己在第一排，就这么一排排回复过去，最后小A就知道自己所在排数了。

另一个比较常见的例子是阶乘的求解，我们知道：$!n = !(n-1) * n$，即 n 的阶乘等于 n-1 的阶乘乘以 n。

这些都是分治策略的典型应用，采用分治法解决问题，包含以下三个步骤：

1. 分解：问题能够分解多个子问题，子问题的形式与原问题相同，只是规模更小。比如上面阶乘的例子，把 n 阶乘的问题，分解为 n-1 阶乘子问题；电影院例子中把“当前第几排”分解为“前排第几排”。这些子问题的特点都是规模在不断缩小。
2. 解决：当问题经过递归的分解之后，子问题规模已经足够小，可以终止递归，直接求解。上面电影院例子中，当到第一排之后，不需要再问前排；阶乘例子中，1的阶乘等于1，即分解到1之后就停止了。
3. 合并：子问题的解能够组合成原问题的解。先说电影院例子，知道前排结果之后，只需要+1就是所求结果；阶乘例子中，知道n-1阶乘之后，乘以n就是所求结果。

递归式

递归式是用来描述递归的，它通常是一个等式或者不等式。上面两个例子，我们可以用文字来描述分治的三个步骤，虽然很详细，但是还是不够直观，下面看看用递归式怎么描述？

• 电影院：

$$\begin{aligned} T(n) = \begin{cases} 1&(n=1)\\ T(n-1)+1&(n>1)\\ \end{cases} \end{aligned}$$

当前排问题 T(n)，可以分解为前排问题 T(n-1)，当递归到第一排时，不需要再进行递归，可以直接求解。

• 阶乘：

$$\begin{aligned} T(n)= \begin{cases} 1&(n=1)\\ T(n-1)*n&(n>1)\\ \end{cases} \end{aligned}$$

递归式是解决递归问题的关键，通过将主问题分解成多个规模更小的子问题，在编写递归函数时，可以认为子问题已经解决（第二步），不要企图在脑子里面一层一层的思考递归怎么执行，那样就会走进思维误区；把关注点放到子问题的分解和合并上（第一、三步），这样能够帮助我们轻松的编写递归代码。

几个例子

爬楼梯问题

再看一个类似的例子，小A上楼要走 n 阶台阶，每一步只能走 1-2 阶，求小A 上楼有多少种走法。

我们先使用暴力枚举法，看看如何解决该问题，这里直接上代码，还是比较容易理解。

function Get_GoUpstairSitCnt(n)
    -- 存储各种走法所走的台阶数
    -- 初始时，第一步有两种走法：1阶、2阶
    local t = nil
    if n > 1 then
      t = {1,2}
    else
      t = {1}
    end

    -- 每走一步，都分为两种情形，即都会增加一种情况
    -- 最多走的步数不会超过台阶数 n
    for i = 1,n do
      local allsituations = #t
      for j=1,allsituations do
        -- 走 1 阶
        if t[j] < n then
          t[j] = t[j] + 1
        end

        -- 走 2 阶
        if t[j] < n then
          table.insert(t,t[j]+1)
        end
      end
    end

    return #t
end

暴力枚举法的时间复杂度具体的我们先不去关心，但是通过嵌套循环就知道复杂度不低，接着尝试用分治策略，看看能不能求解该问题。下面按照分支策略步骤一步步来分析。

1. 分解问题，要走 n 阶台阶，初始时能够确定的只有第一步的走法：1阶、2阶，走完第一步，那么剩下的怎么走呢，能够发现这个和主问题是一样的，只不过台阶减少了，即问题的规模变小了，因此可以采用递归来解决。通过上面分析，我们得到两个子问题：
   1. 第一步走 1 阶，剩余台阶的走法
   2. 第一步走 2 阶，剩余台阶的走法
2. 解决问题，上面两个问题都是采用递归来解决，解决递归就是要找到它的终止条件，考虑一下，什么时候递归可以停止呢？
   1. 剩余 1 阶，只有 1 种走法
   2. 剩余 2 阶，只有 2 种走法
3. 合并，将两种子问题结果相加，就是主问题的解。

经过上面的分析，应该能够很容易的写出递归式了。

$$T(n)=\begin{cases} 1&(n=1)\\ 2&(n=2)\\ T(n-1)+T(n-2)&(n>2) \end{cases}$$

有了递归式，代码就很容易写了：

function T(n)
  if n == 1 then
    return 1
  elseif n==2 then
    return 2
  end
  
  return T(n-1)+T(n-2)
end

求解最大数组

再看一个复杂一点的例子，一个包含正负元素的数组，求它的连续子数组中，元素求和值最大的子数组。例如下面一个数组：

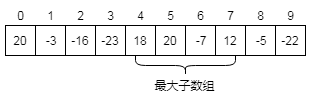
解决这个问题的办法有很多，最简单暴力的方法，就是遍历各种可能性，然后查找最大值，代码如下：

--- Lua示例
--- 查找最大子数组
--- 因为 Lua 数组下标从 1 开始，所以输出的结果为：43、5、8
function Find_Max_Subarray(arr)
  local low,high
  local max = math.mininteger
  
  local sum = 0
  
  for i = 1,#arr do
    sum = 0
    for j = i,#arr do
      sum = sum + arr[j]
      if sum > max then
        max = sum
        low = i
        high = j
      end
    end
  end
  
  return max,low,high
end

这段代码的渐进复杂度为$T(n) = O(n^2)$，可以看到暴力枚举法的复杂度比较高，通过分治策略，看看能不能找到其他的解决办法。根据分治策略的执行步骤，我们尝试着来做一下：

1. 首先需要对问题进行分解，即缩小问题规模，我们可以简单的把数组均分，那么问题就变成了，如何在两个分数组中查找最大子数组。这里可以分为三种情况，可能在左侧分数组、可能在右侧分数组、可能跨越两个数组，考虑这三种情况，可以得到四个子问题：
   • 在左侧分数组中，查找最大子数组
   • 在右侧分数组中，查找最大子数组
   • 跨越左右分数组，查找最大子数组
   • 比较前面三种问题的解，得到最优的解

在上面四个子问题中，前两种个和主问题相同，都是求一个数组的最大子数组，只不过数据规模变小了，可以采用递归来计算。

1. 第二步需要解决子问题，这里子问题有四个，但是前两是相同的。先考虑前两个子问题的怎么解决，随着问题规模不断的递归分解，最终需要求解的数组元素只有一个了，此时子问题已经足够简单，可以直接给出解，终止递归；第三个子问题是从两个数组中，找到横跨两个数组的最大数组，该子问题与主问题已经主问题不同了，所以这里就没有必要递归了，直接求解即可，代码见下；最后一个子问题，和主问题也不相同，所以直接求解。
2. 最后一步是合并，这一步比较简单，就是根据前三个子问题的解，在第四个子问题中进行比较，得出主问题的解。

使用递归式描述如下：

$$T(arr,low,high)=\begin{cases} arr[low]&(low = high)\\ max(T(arr,low,mid), T(arr,mid,high),G(arr,low,mid,high))&(low < high,mid = \left \lfloor {(low + high)/2} \right \rfloor) \end{cases}$$

这里先给出第三个子问题的求解的 Lua 代码：

function Find_Max_Cross_Subarray(arr,low,mid,high)
  -- 保存最大子数组的起始索引
  local left_index,right_index
  local leftMax = math.mininteger
  local rightMax = math.mininteger
  
  -- 查找左侧最大子数组
  local sum = 0
  for i = mid,low,-1 do
    sum = sum + arr[i]
    if sum > leftMax then
      leftMax = sum
      left_index = i
    end
  end
  
  -- 查找右侧最大子数组
  sum = 0
  for i = mid+1,high do
    sum = sum + arr[i]
    if sum > rightMax then
      rightMax = sum
      right_index = i
    end
  end
  
  -- 合并两边
  return leftMax+rightMax,left_index,right_index
end

第三个子问题解决之后，因为前两个子问题与主问题相同，而最后一个子问题又需要前三个子问题的结果，所以这里就直接求解主问题，直接上 Lua 代码。

function Find_Max_Subarray_Recursion(arr,low,high)
  -- 当递归不断执行，进行一段时间之后，数组只剩一个元素，此时不需要再进行递归，可以直接得出结果
  if low == high then
    return arr[low],low,high
  else
    -- 将数组分为左右两部分，即将问题分解为更小规模子问题
    -- 将中间值向下取整
    local mid = (low + high) // 2

    -- 左侧分数组求解
    local leftMax,leftLow,leftHigh = Find_Max_Subarray_Recursion(arr,low,mid)

    -- 右侧分数组求解
    local rightMax,rightLow,rightHigh = Find_Max_Subarray_Recursion(arr,mid+1,high)

    -- 跨越左右分数组求解
    local crossMax,crossLow,crossHigh = Find_Max_Cross_Subarray(arr,low,mid,high)

    -- 比较三种问题的解，得出最大子数组
    if leftMax > rightMax and leftMax > crossMax then
      return leftMax,leftLow,leftHigh
    elseif rightMax > leftMax and rightMax > crossMax then
      return rightMax,rightLow,rightHigh
    else
      return crossMax,crossLow,crossHigh
    end
  end
end

递归中的重复计算问题

还是看上面爬楼梯的例子，其中包含了很多重复的计算，随着 n 值的减小，重复的次数呈指数级递增，以 n = 6 为例，通过下面的图示，对重复计算有个直观了解。

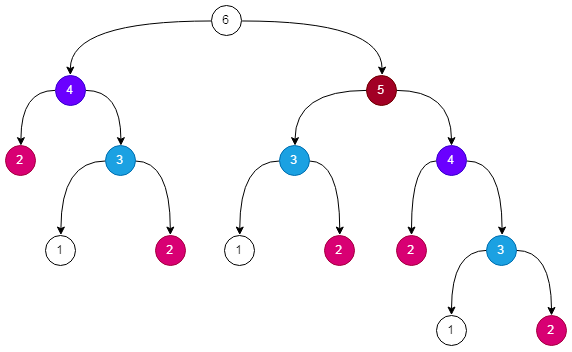
从上图可以看出来，对 n = 2 计算了 5 次，n = 3 计算了 3 次，如果 n 增长到7，6结点下面的所有结点重复次数将会递增 1 倍，这种指数级的重复增长，是对资源的极大浪费，一个解决办法就是采用缓存，将计算过结果缓存起来，爬楼梯的例子修改如下：

local cache = {}
function T(n)
  if n == 1 then
    return 1
  elseif n==2 then
    return 2
  end
  
  if cache[n] ~= nil then
    return cache[n]
  end

  local count = T(n-1) + T(n-2)
  cache[n] = count
  return count
end

根据递归式计算时间复杂度

递归式的一个非常重要的应用，是用来计算递归算法的时间复杂度，在《算法导论》一书中介绍了三种根据递归式来计算时间复杂度的解法。分别是：

• 代入法
• 递归树法
• 主方法求解递归式

代入是首先要求对递归式的解作出猜测，然后将猜测的值代入递归式进行验证，所以这就要求计算着对数学公式比较敏感，否则比较难猜测出正确的解；递归树法是将递归过程，利用树形结构进行表示，然后通过观察树的结构，来对解作出猜测，再将猜测结果代入递归式进行验证；这里主要介绍第三种方法，通过递归式的主方法来进行求解。

主方法求解是将递归式表示成如下形式：

$$T(n)=aT(n/b) + f(n)$$

以上递归式描述是这样的：将一个规模为 n 的问题分解为 a 个子问题，每个子问题的规模为 $n/b$，时间复杂度为 $T(n/b)$；$f(n)$是子问题分解、组合所花费的时间。

需要注意的是，这里 $n/b$ 可能不为整数，但是替换成 $T(\left \lfloor n/b \right \rfloor)$或$T(\left \lceil n/b \right \rceil)$对渐进时间复杂度并不会产生影响，所以后续的计算都是忽略舍入问题的。

主方法依赖于下面的主定理：

令$a\geqslant{1}、b>1$是常数，$f(n)$是函数。则对于递归式：

$$T(n)=aT(n/b)+f(n)$$

$T(n)$的渐进复杂度满足下面三种情况：

$$T(n)=\begin{cases} \Theta(n^{\log_{b}^{a}})&f(n)=O(n^{\log_b^{a-\varepsilon}}),{\varepsilon}>0\\ \Theta(n^{\log_{b}^{a}}{\lg}n)&f(n)=\Theta(n^{\log_b^a})\\ \Theta(f(n))&f(n)={\Omega}(n^{\log_b^{a+\varepsilon}}),{\varepsilon}>0\\ \end{cases}\\$$

主定理根据 $f(n)$ 与 $n^{\log_b^a}$ 的关系，分为三种情况，首先T(n)的渐进复杂度是由两者之间较大的值决定的，若 $n^{\log_b^a}$ 更大，则为第一种情况；若$f(n)$更大，则满足第3种情况；若两者值相当，则满足第2种情况，对 $n^{\log_b^a}$ 乘上一个对数因子。

需要注意的是，f(n)与$n^{\log_b^a}$两者比较的是渐进界，对于两者的渐进界比较结果和多项式比较结果如果不一致，说明此时不在上面三种情况之中，因此此时就主定理就不再适用。

通过两个例子，看看主方法怎么用。

先看第一个例子：

$$T(n)=9T(n/3)+n$$

• 首先，对于这个递归式，可以知道$a=9,b=3,f(n)=n$
• 然后，比较$f(n)=n$、$n^{\log_b^a}$=$n^{\log_3^9}$=$n^3$ 两者的渐进界，符合第一种情况，因此

$$T(n)=\Theta(n^{\log_{b}^{a}})=\Theta(n^{\log_3^9})=\Theta(n^2)$$

再看第二个例子：

$$T(n)=T(2n/3)+1$$

• 首先，根据递归式可知：$a=1,b=3/2,f(n)=1$
• 然后，比较 $f(n)=1$ 和 $n^{\log_b^a}$ = $n^0$ = 1 比较两者的渐进界，满足第2种情况，因此:

$$T(n)=\Theta(n^{\log_{b}^{a}}{\lg}n)=\Theta(\lg{n})$$

关于主方法这部分内容，详细可以参考《算法导论》的第四章，里面给出了更加详细的介绍和证明。