数据结构与算法 - 栈
栈是一种后进先出的数据结构,栈的常见操作包括入栈(Push)、出栈(Pop),栈就好像一摞盘子,每次放盘子总是放到最上面,同样每次也是从最上面取。
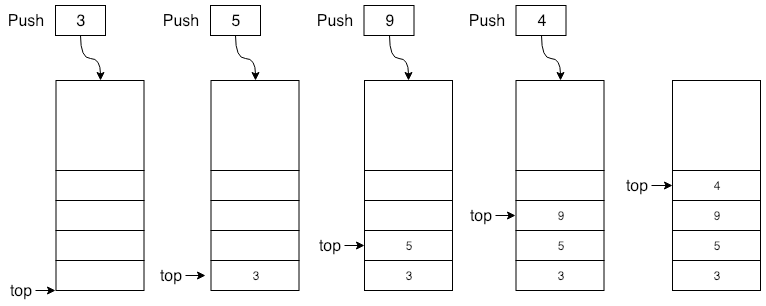
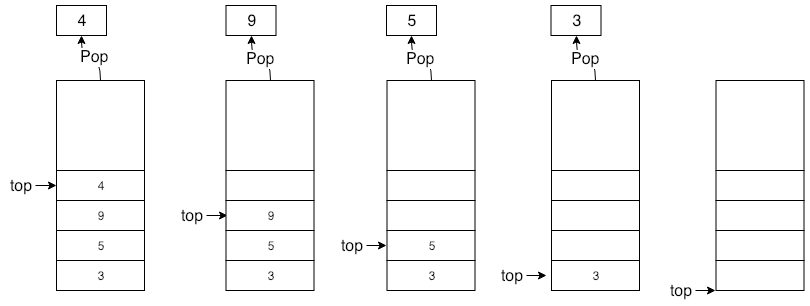
栈的实现
可以使用数组或者链表来实现栈结构,本文采用基于数组的链表实现,下面主要实现栈的入栈、出栈、查询栈顶元素等操作。
入栈:
1 | public void Push(T item) |
出栈:
1 | public T Pop() |
完整代码在这里。
应用场景
栈这种数据结构在日常开发中还是比较常用的,主要的应用场景包括:
- 函数调用
- 表达式求值
- 括号匹配
函数调用
在进行单步调试时,可能经常会看到调用栈这个东西,正如它的名字所指,它是一种栈结构,我们通过一段代码来简单看下它是如何工作的。
1 | int main(){ |
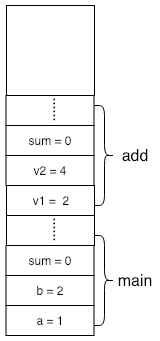
表达式求值
编译器通常利用两个栈来实现表达式的计算,其中一个栈用来保存操作数,另一个栈来保存操作符。
开始时,从左向右遍历表达式,当遇到操作数时,直接压入操作数栈;当遇到运算符时,就需要与操作符栈顶元素进行比较,如果栈顶元素优先级高,将当前运算符入栈;如果比栈顶元素优先级低或者相同,取出栈顶运算符,从操作数栈取出相应数量的操作数,然后进行计算,最后把计算结果压入操作数栈,继续执行比较。
下面通过一个流程图来帮助一下理解。
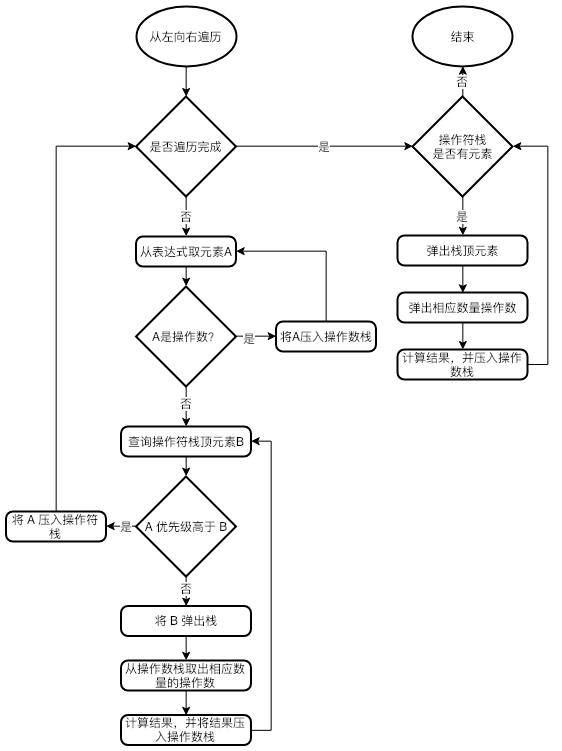
这里有一个非常简单的示例
括号匹配
假如要解析字符串,其中包括圆括号()、方括号[]、大括号{},它们必须成对出现,并且可以相互嵌套。那么如何检测括号是否合法呢?
用栈这种数据结构能够非常简单的解决此问题,同样需要从左往右遍历字符串,遇到左括号时,直接入栈;遇到右括号,与栈顶元素是否成对儿,成对儿则弹出,否则不合法;字符串遍历完成之后,如果栈不为空,则不合法。
流程图如下: