数据结构与算法 - 链表

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

数据结构与算法 - 链表

在日常的开发中，链表是一种非常常用的数据结构，与数组相同，链表也是一种线性列表，与数组不同的是，数组元素的顺序由下标来决定，链表的下标则通过指针来决定。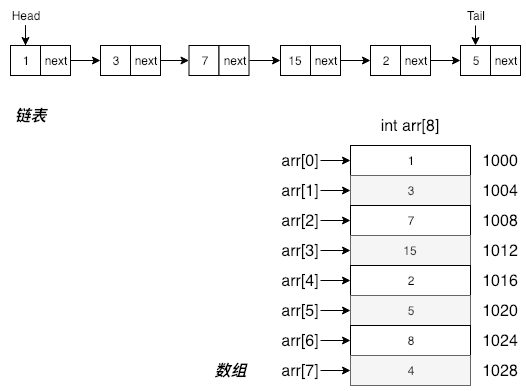

通过上图可以看出，数组和链表主要存在以下几点不同：

  1. 链表是由一个个结点组成，每个结点都保存着指向下个结点的指针；数组的线性顺序由下标决定。
  2. 数组的地址是连续的，但是链表的结点则不连续。（连续地址带来的好处时可以缓存）

常用操作

对于集合类型来说，最常用的操作就是插入、删除和查找。在执行这些操作时，通常有两种情况，以删除操作为例：

  1. 已知要删除的结点对象。
  2. 已知结点存储的值。这种情况下，需要先找到对应的结点。

数据插入

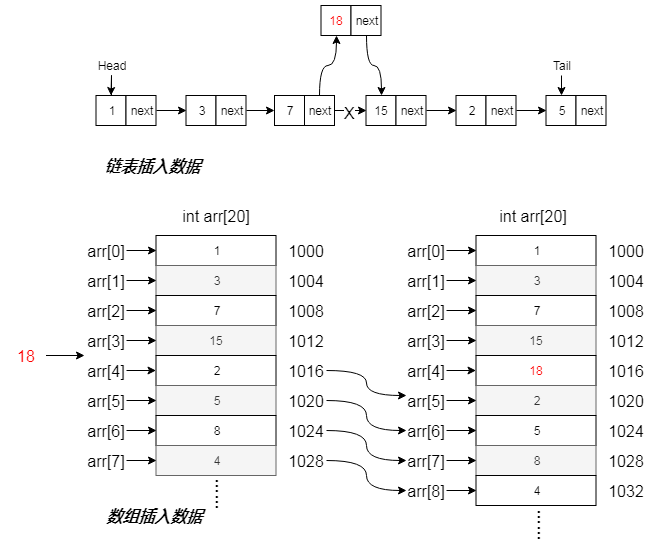
向数组中插入数据，分为两种情况：

  1. 数组没有空闲位置，此时需要为数组重新分配一块更大的连续内存，并且分配完成之后，需要将数组元素拷贝到新数组中。
  2. 数组有空闲位置，此时需要将插入位置之后的数组元素，向后拷贝移动，为新元素腾出位置。

向链表中插入数据，假设要在结点 A、B 之间插入一个新结点 C，那么只需要将 A 的指向下个结点的指针，使之指向 C 结点，C 结点指向 B 结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//链表插入部分代码
public LinkedNode<T> InsertAfter(int position, T item)
{
   if (position < 0 || position > length)
   {
       throw new IndexOutOfRangeException("position out of index");
   }

   var p = head;
   int j = 1;
   while (p != null && j < position)
   {
       p = p.next;
       j++;
   }

   var newNode = new LinkedNode<T>(item);
   newNode.next = p.next;
   p.next = newNode;

   length++;

   return newNode;
}

分析这段代码的复杂度：

  • 最好情况：O(1)
  • 最坏情况: O(n)
  • 均摊复杂度：O(n)

需要注意的是，这里最坏情况和均摊时间复杂度之所以为 O(n)，是因为在进行删除之前进行索引，如果知道在哪个结点下面进行插入，那么复杂度将变为 O(1)，见下面代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public LinkedNode<T> InsertAfter(LinkedNode<T> node, T item)
{
    if (position < 0 || position > length)
    {
        throw new IndexOutOfRangeException("position out of index");
    }

    if (head == null)
    {
        head = new LinkedNode<T>(item);
        length++;
        return head;
    }
    else
    {
        var p = head;
        int j = 1;
        while (p != null && j < position)
        {
            p = p.next;
            j++;
        }

        var newNode = new LinkedNode<T>(item);
        newNode.next = p.next;
        p.next = newNode;

        length++;

        return newNode;
    }
}

数据删除

通过上图可以看到，与数据的插入类似，如果已知要删除的结点，首先需要找到它的前置结点，然后将前置结点的指针指向要删除结点的下个结点，代码示例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public void Remove(LinkedNode<T> node)
{
    //处理Null情况
    if (node == null)
        return;

    //空链表
    if (head == null)
        return;

    if (node == head)
    {//要处理的结点为头结点
        var h = head;
        head = head.next;
        h.next = null;
    }
    else
    {
        var p = head;
        while (p.next != null && p.next != node)
            p = p.next;

        if (p == null)
            return;

        p.next = node.next;
        node.next = null;
    }

    length--;
}

复杂度分析：

  • 最好情况复杂度：O(1)
  • 最坏情况复杂度：O(n)
  • 均摊情况复杂度：O(n)

边界处理

一般编写代码，最容易出现错误的地方就是边界情况和异常情况，在实现链表时尤其如此，因此，在编写链表代码时，要把边界情况处理全面。常见的一些边界条件如下：

  • 链表为空
  • 链表只包含一个、两个结点
  • 要处理的结点是头结点、尾结点

通过设置哨兵，可以简化边界的处理，并且可以是代码变得更加简洁。哨兵通常是一个哑对象，它的下一个结点指针通常指向链表的头结点或者尾结点。我们利用哨兵来对删除操作进行修改：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
headNil = new LinkedNode(default(T));

public void Remove(LinkedNode<T> node)
{
    if (node == null)
        return;

    var p = headNil;
    while (p.next != null && p.next != node)
        p = p.next;

    if (p == null)
        return;

    p.next = node.next;
    node.next = null;

    length--;
}

复杂度分析：

  • 最好情况复杂度：O(1)
  • 最坏情况复杂度：O(n)
  • 均摊情况复杂度：O(n)

哨兵的主要作用是简化边界处理，并不能够降低渐进时间复杂度（会降低渐进复杂度的系数）。因为每个链表都需要额外的空间来保存哨兵，比如对于需要大量小链表的情景，就会造成内存空间的浪费。

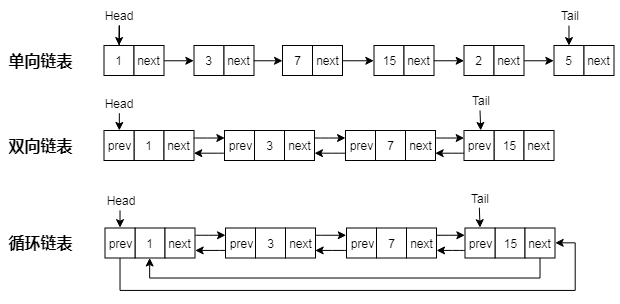
常见的链表

链表的种类很多，可以是单向链接或者双向链接，单向链接每个结点只存储下一个结点的指针(next)，而双向链接还存储了上一个结点的指针(prev)；也可以是循环或者非循环的，循环链表的最后一个结点的next指针指向链表的第一个结点；可以是已排序或者未排序的，具体的链表结果可以看下图，分别展示了单向非循环链表、双向非循环链表、双向循环链表。

最后附上源码。