3D中的方位与角位移
在三维空间中,描述物体的旋转状态有多种方式,这些方式中,可能选取的参考坐标系不同、也可能选取的基向量不同,或者是采用的数学表达方式不同,等等,这些差异就造成理解三维旋转比较困难。本文通过梳理常见旋转描述方式,希望能够帮助理解三维空间中的角位移。
坐标系选择
当我们描述一个物体的坐标时,首先需要选定参考坐标系,通常是世界坐标系的原点;同样的,我们在描述一个物体的旋转时,也需要选定一个参考坐标系,这里通常选择惯性坐标系。
惯性坐标系:惯性坐标系的原点与物体坐标系重合,但是坐标轴与世界坐标系平行。
为什么引入惯性坐标系:惯性坐标系到物体坐标系只需要进行旋转,惯性坐标系到世界坐标系是需要平移,将世界坐标系到物体坐标系的转换过程分解为两个步骤进行,能够简化问题。
旋转变换表示
在选定好参考坐标系之后,就需要确定,从参考坐标系(惯性坐标系)到物体坐标系之间的变换如何表示,这里通常有三种方式:
- 矩阵
- 欧拉角
- 四元数
这三种方式有个优略,对于各个游戏引擎来说,针对不同的使用场景可以选取不同的表示方式。下面就针对这三种方式,进行详细分析比较,来加深对旋转的理解。
矩阵表示旋转
构建旋转矩阵的关键在于,计算旋转矩阵的基向量,得到基向量之后,就可以组成旋转矩阵,该矩阵的意义表示从一个坐标系到目标坐标系的旋转。光看描述可能还是比较难理解,看一个具体的例子,为了简化问题,这里只进行绕$y$轴的旋转。
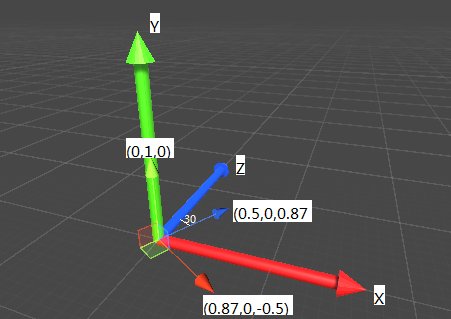
很容易计算得到三个基向量:
对应的旋转矩阵为:
该矩阵就表示从参考坐标系(惯性坐标系)到目标坐标系(物体坐标系)的旋转变换,参考坐标系中的任意向量$v$,都可以通过与矩阵相乘$(v*M)$,得到旋转之后的向量。
通过上面例子可以看到矩阵表示旋转的一些优缺点,总结如下:
优点:
- 不需要关注旋转的顺序,因为整个矩阵就是一个整体,直接乘以该矩阵,就可以实现向量的旋转。
- 利用矩阵的逆矩阵,可以实现旋转的撤销(反向旋转)。
- 可以合并多个旋转矩阵,矩阵$M_1$表示坐标系A 到 B 的旋转,矩阵$M_2$坐标系 B 到 C 的旋转,那么矩阵$M_1 * M_2$表示A 到 C 的旋转。
- 最后一点是图形 API 都采用矩阵的形式来表示旋转。
缺点:
- 矩阵的表示形式比较浪费内存,矩阵使用 9 个参数来表示,和后面介绍的欧拉角和四元数来说,内存占用比较高。
- 矩阵难以使用,给定一个矩阵之后,并不能直观的知道矩阵表示一个怎样的旋转。
- 矩阵可能是病态的,旋转矩阵为正交矩阵,在变换的过程中,可能由于浮点数的精度问题,导致“矩阵蠕变”,从而导致病态矩阵。
欧拉角表示
欧拉角的基本思想是将旋转分解为,绕三个相互垂直轴的旋转组成的序列。这句话读起来非常拗口,其实非常易于理解。注意到定义中的几个要点,首先是三个绕垂直轴旋转的分量,这三个轴可以是任意的三个轴,但是通常选择笛卡尔坐标系比较有意义;其次是三个分量的顺序,这里也没有进行规定,因此可以是任意的顺序,其中有些顺序比较常用,因此人们为它起了名字,比如“head-pitch-bank”、“roll-pitch-yaw”等等。
通过例子来看下”head-pitch-bank”是如何进行旋转的。
- 初始时,物体坐标系与惯性坐标系重合,红色-X轴、绿色-Y轴、蓝色-Z轴。

- 首先进行Heading 旋转,heading 为绕 y 轴的旋转分量,根据左手定则进行旋转 45 度。

- 然后进行Pitch 旋转,Pitch 为绕 x 轴的旋转分量,需要注意的是,这里的 x 轴选取的是物体坐标系的 x 轴,而非惯性坐标系。

- 最后是进行Bank 旋转,Bank 是绕 z 轴的旋转分量,同样的,这里的 z 轴是物体坐标系的 z 轴,而非惯性坐标的 z 轴。

其他欧拉角旋转方式
在前面提到,欧拉角的轴和旋转顺序的选取多种多样,“Head-pitch-bank” 只是其中的一种,还有一种比较常见的旋转方式为“Roll-pitch-yaw”,其中roll 为绕 z 旋转的分量,pitch 为绕 x 轴旋转的分量,yaw 为绕 y 轴旋转的分量,Unity3D 中就采用这种欧拉角约定。
如果需要在两种不同约定之间进行转换,最简单的方式是通过矩阵。
欧拉角的优缺点
优点:
- 很容易使用,从上面例子就可以看到,欧拉角非常的直观,并且符合人类思维方式。
- 描述简洁,欧拉角只需要三个参数,就能够描述一个旋转。
- 任意三个数都是合法的欧拉角
缺点:
- 别名问题,即给定一个方位,有多种欧拉角可以描述它
- 最常见的是任意角度加上$360^o$,都等于它自身。
- 另一个别名问题是,$pitch135^o$ 等价于$heading180^o、pitch45^o、bank180^o$。
- 最著名的别名问题是,先$heading45^o、pitch90^o$ 等价于$pitch90^o、bank45^o$,事实上只要第二个旋转轴旋转${\pm}90^o$,那么第一个轴就会和第三个轴重合,这种现象称为“万象锁”。
解决别名问题,一般通过限制各个旋转分量的范围,比如对于“heading-pitch-bank”约定来说:
heading、bank限定在 $-180^o\sim180^o$,pitch限定在$-90^o\sim90^o$。
“万象锁”解决办法:$当pitch=\pm90^o时,bank=0^o$
- 欧拉角的第二个问题是,两个角度之间的插值非常困难。在开发中,经常需要将摄像机平滑的进行旋转,比如从旋转 $\theta_0$ 插值到旋转 $\theta_1$,根据线性插值公式
插值可能会存在很多问题,如果欧拉角没有进行限制,将得到很大角度差,假设 $\theta_0=45^o,\theta_1=720^o$,因为720 = 360*2 + 0,所以$\theta_0、\theta_1$两个角度之间只相差$45^o$,但是根据线性插值公式计算,$\Delta\theta=\theta_1-\theta_0=675^o$,旋转了将近两周!解决这个问题的方法就是采用上面的角度限制方法,对欧拉角进行限定。
然而,即使对角度进行了限定,仍然不能完全解决插值问题,这是由于旋转角度的周期性引起的。看下例子,$假设\theta_1=170^o、\theta_0=-170^o$,值都在限定的范围内,但是插值的结果仍然是不正确的,旋转沿着长弧旋转了$340^o$,而非短弧旋转的$20^o$。解决该问题的方法是将 $\Delta\theta$ 限制到$-180^o\sim180^o$,公式为:
然而,即使有了这两个限定,仍然会遇到“万向锁”问题,插值的前两个问题可以通过角度限定来解决,但是“万向锁”是一个底层的问题,目前来说没有办法来解决它。
四元数表示
前面介绍了旋转的矩阵和欧拉角表示方法,也介绍了这两种方式的优缺点,下面介绍第三种旋转的表示方法-四元数,它在一定程度上集中了矩阵和欧拉角的有点,它采用4个参数来表示,并且能够解决欧拉角中的“万向锁”问题,下面就详细的了解一下四元数。
复数
在正式介绍四元数之前,还是需要先介绍一下复数,复数对$(a,b)$表示$a+bi$,其中$a$称作实部,$b$称作虚部,$i$为虚数,满足$i^2 = -1$。下面可能采用$(a,b)$和$a+bi$两种表达形式,两者是等价的。
复数性质
对于复数$a+bi$,它具备如下性质:
- 复数相加:$(a+bi)+(c+di) = (a+c)+(b+d)i$
- 复数相减: $(a+bi)-(c+di) = (a-c)+(b-d)i$
- 复数相乘:
- 共轭:复数的共轭就是让虚部变负,即$p=a+bi$的共轭复数为${p}^*=a-bi$。
- 模:
复数的几何意义
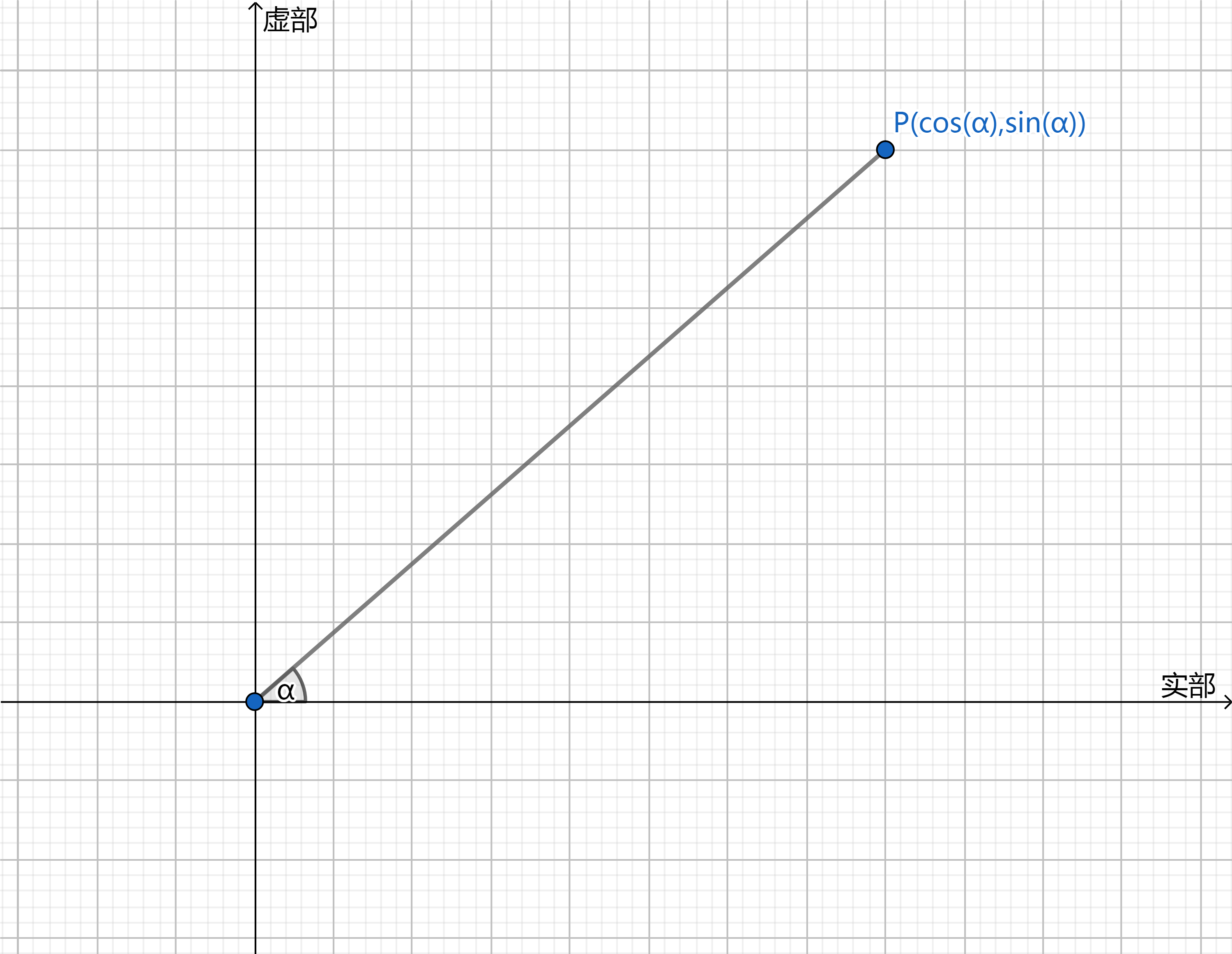
复数包括实部和虚部两部分,如果把实部当作横轴、虚部当作纵轴,这样复数就能表示平面内的任意点,如果把该点到原点的向量,当作是横轴正向旋转一定角度后的结果,那么复数就可以表示旋转!
如下图所示,复数$p = \cos\alpha +i*\sin\alpha$,它表示的旋转角为$\alpha$。
扩展复数
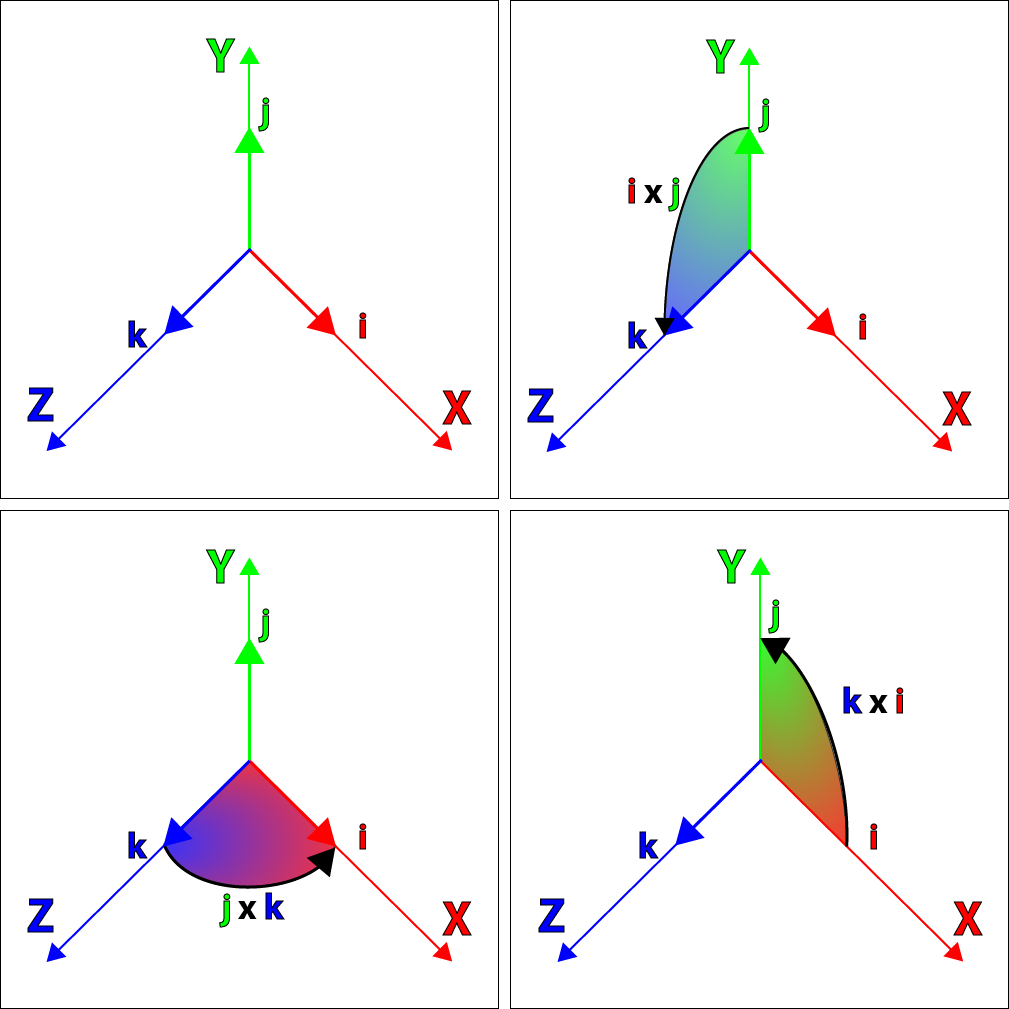
我们知道,一个物体在三维空间的方位,都能通过物体绕轴旋转一个角度来达到。那么既然复数能够表示二维空间的旋转角度,那么能不能扩展到三维空间呢,这个问题也困扰了数学家们很久,直到1843年,爱尔兰数学家$William Hamilton$ 才解决这个问题,这就产生了四元数的概念,他通过采用三个虚部来实现3D空间旋转的表示,即四元数$\left [ w,\left ( x,y,z \right ) \right ] w,x,y,z \in \mathbb{R}$定义了复数 $w + xi + yj + zk$,其中$i,j,k$的关系如下:
可以看到,i、j、k之间的关系,既保留了复数的性质,同时,和笛卡尔坐标系的三个基坐标轴的叉乘关系非常像,对比下图(右手坐标系)。
四元数相关的性质
四元数的表示形式
四元数是复数的一种扩展形式,很多复数的性质,四元数也都满足。在介绍四元数性质之前,再重复一下四元数的表示形式,这两种形式都是等价的,只不过复数形式方便进行计算,向量的表示便于记忆和书写:
- 向量表示形式:$q=\left [ w,\vec{v} \right]$或者$q=\left [ w,\left ( x,y,z \right ) \right ]$
- 复数表示形式:$q=w + xi + yj + zk$
实四元数与纯四元数
实四元数是所有虚部向量为零向量的四元数:
- 向量形式:$q=[w,(0,0,0)],或者q=[w,0]$
- 复数形式:$q=w+0i+0j+0k=w$,可以看到实数可以写成实四元数的形式!
纯四元数是实部为零的四元数:
- 向量形式:$q=[0,(x,y,z)]$
- 复数形式:$q=xi+yj+zk$
单位四元数
在向量中,任何向量都可以用长度和单位向量方向来表示:$\vec{v}=l*\vec{n}$,其中$l=|\vec{v}|$,$\vec{n}$是$\vec{v}$同方向的单位向量$|\vec{n}|=1$。
四元数加法
四元数的系数缩放
- 向量表示形式:
- 复数表示形式:
四元数的乘法(叉乘)
有两个四元数:${q}_1、{q}_2$,计算它们的乘积:
知道了四元数乘法的定义之后,这里还有几条乘法相关的性质:
- 乘法满足结合律,但是不满足交换律:$(ab)c=a(bc),ab \neq ba$
- 乘积的模等于模的乘积:$||q_1\cdot{q}_2||=||q_1|| \cdot ||q_2||$
- 乘积的逆等于逆的反向乘积:$({q_1q_2})^{-1}={q_2}^{-1}{q_1}^{-1}$
四元数的点乘
四元数的点乘的定义和向量的点乘类似:
对于单位四元数来说,点乘结果的取值范围是$(-1\sim{1})$,它的几何意义与向量类似,它的绝对值越大,表示这两个四元数代表的旋转越相似。
四元数的共轭
四元数的共轭就是把虚部向量取负,记作:${q}^*$
- 向量形式:$q^*=[w,-(x,y,z)]$
- 复数形式:$q^*=w-xi-yj-zk$
四元数的模
四元数的模定义为:
- 复数形式:$||p||=\sqrt{w^2+x^2+y^2+z^2}$
- 向量形式:$||p||=\sqrt{w^2+||\vec{v}||^2}$
模的平方定义为:$||p||^2=pp^*=w^2+x^2+y^2+z^2$
四元数的逆
四元数的逆记为:$q^{-1}$,满足以下性质:
四元数逆的几何意义和矩阵的逆类似,可以用来表示一个旋转的逆向旋转。
四元数表示三维旋转
上面说了很多四元数的性质,但还是看不到四元数是怎么表示三维空间中的旋转的,下面直接上公式,下面旋转表示绕旋转轴$n$旋转$\theta$: